Question

已知α是三角形的内角,且sinα+cosα=,求tanα的值.

Answer 1

解:由sinα+cosα=平方整理,得sinαcosα=-＜0.

∵α为三角形的内角,∴0＜α＜π,sinα＞0,cosα＜0.

∴sinα-cosα＞0.

∵(sinα-cosα)²=1-2sinαcosα=,

∴sinα-cosα=.

由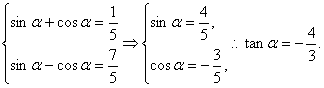

点拨:本题主要考查同角三角函数的基本关系式.对于三角求值题目,一定要注意角的范围,有时要根据所给三角函数值的大小,适当缩小所给角的范围,才能求出准确的值.教师要抓住时机就此进一步挖掘,以激起学生的探究兴趣.如本题又可改为:已知α是三角形的内角,且sinα+cosα=,则tanα的值为(    )

A.                 B.                    C.-                  D.-

    改编成选择题后,教师引导学生结合三角函数线及题目给出的条件特点探究角的范围.并启发学生思考讨论能否小题不大做,不用计算就能解出来.

事实上,若0＜α＜,则sinα+cosα＞1,但sinα+cosα＝,

    所以＜α＜π,且知sinα＞0,cosα＜0,|sinα|＞|cosα|.因此tanα＜-1,

    所以不用运算就选出了答案.这就是解选择题的方法,找准特征,抓住关键,快速准确.