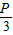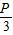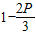Question

设离散型随即变量X的分布列为 X 0 1 2 P P 3 P 3 1- 2P 3 则X的数学期望的最小值为（　　）

• A．0
• B．

  1

  2

• C．2
• D．随p的变化而变化

Answer 1

分析：由于已知分布列求出P的取值范围，再使用期望公式先求出数学期望的表达式，进而根据一次函数的图象和性质，得到数学期望的最小值

解答：解：∵0≤1-

2P

3

≤1，0≤

P

3

≤1，
∴0≤P≤

3

2

E（x）=0×

P

3

+1×

P

3

+2×（1-

2P

3

）=2-P
当P取最大值

3

2

时，E（x）取最小值

1

2

故选B

点评：本题主要考查离散型随机变量的分布和数学期望、使用期望公式先求出数学期望的表达式，是解答本题的关键．