题目内容
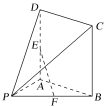
【题目】在如图所示的几何体中,四边形ABCD是正方形,PA⊥平面ABCD,E,F分别是线段AD,PB的中点,PA=AB=1.
(1)证明:EF∥平面PDC;
(2)求点F到平面PDC的距离.
【答案】(1)证明见解析(2)![]()
【解析】
(1)把![]() 向上平移,
向上平移,![]() 与
与![]() 重合,则
重合,则![]() 应在
应在![]() 上,因此得辅助线作法,取
上,因此得辅助线作法,取![]() 中点
中点![]() ,连接
,连接![]() ,只要证明
,只要证明![]() 即可证线面平行;
即可证线面平行;
(2)由(1)只要求![]() 到平面
到平面![]() 的距离即可,这可用体积法求解,即
的距离即可,这可用体积法求解,即![]() .
.
(1)证明取PC的中点M,连接DM,MF,
∵M,F分别是PC,PB的中点,∴MF∥CB,MF=![]() CB,
CB,
∵E为DA的中点,四边形ABCD为正方形,
∴DE∥CB,DE=![]() CB,
CB,
∴MF∥DE,MF=DE,∴四边形DEFM为平行四边形,
∴EF∥DM,∵EF![]() 平面PDC,DM
平面PDC,DM![]() 平面PDC,
平面PDC,
∴EF∥平面PDC.
(2)解∵EF∥平面PDC,∴点F到平面PDC的距离等于点E到平面PDC的距离.
∵PA⊥平面ABCD,∴PA⊥DA,在Rt△PAD中,PA=AD=1,∴DP=![]() .
.
∵PA⊥平面ABCD,∴PA⊥CB,∵CB⊥AB,PA∩AB=A,∴CB⊥平面PAB,
∴CB⊥PB,则PC=![]() ,∴PD2+DC2=PC2,
,∴PD2+DC2=PC2,
∴△PDC为直角三角形,
∴S△PDC=![]() .
.
连接EP,EC,易知VE-PDC=VC-PDE,设E到平面PDC的距离为h,
∵CD⊥AD,CD⊥PA,AD∩PA=A,∴CD⊥平面PAD,
则![]() ×h×
×h×![]() =
=![]() ×1×
×1×![]() ×
×![]() ×1,∴h=
×1,∴h=![]() ,
,
∴点F到平面PDC的距离为![]() .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目


