题目内容
若二次函数的图象的对称轴方程为x=1，则m=分析：由二次函数对称轴方程解得m=1，将m=1代入二次函数解析式得到函数解析式，再用顶点坐标公式得出顶点坐标，由图象可知函数的单调增区间．
解答：解：由对称轴方程x=-
=-
=1得m=1，将m=1代入y=x2+2mx-m2-2得y=x2+2x-3，再将x=1代入函数解析式得y=-4
即顶点坐标为（1，-4），又由函数的对称轴是x=1且函数开口向上可知：函数的递增区间为（1，+∞）．
| b |
| 2a |
| 2m |
| 2 |
即顶点坐标为（1，-4），又由函数的对称轴是x=1且函数开口向上可知：函数的递增区间为（1，+∞）．
点评：本题考查的是二次函数的基础知识．
练习册系列答案
相关题目
。
，都有
，求证：关于x的方程
有两个不相等的实数根且必有一个根属于（
）；
成等差数列，设函数f (x)的图象的对称轴方程为
，求证：
。
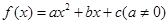的图象和直线
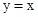无交点，现有下列结论：
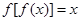一定没有实数根；
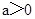，则不等式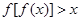
对一切实数x都成立；
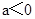，则必存在实数
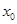，使
;
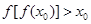的图象与直线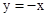
一定没有交点，
的图象与x轴有两个不同的公共点，且
，当
时，恒有
.
时，求不等式
的解集；
,求a的值；
，且
对所有
恒成立，求正实数m的最小值.
的图象和直线y=x无交点，现有下列结论：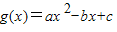
的图象与直线y=-x也一定没有交点．
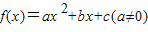的图象和直线y=x无交点，现有下列结论：
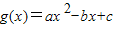的图象与直线y=-x也一定没有交点．