题目内容
(本题满分13分)
设![]() ,
,![]() ,且
,且![]() 中元素满足:对任何
中元素满足:对任何![]() ,恒有
,恒有![]() .
.
(1)试说明:集合![]() 的所有元素之和必为偶数;
的所有元素之和必为偶数;
解析:(1)将集合![]() 的所有元素分组为
的所有元素分组为![]() 、
、![]() 、……、
、……、![]() 、
、![]() ,共100组;由已知得,集合
,共100组;由已知得,集合![]() 的100个元素只能从以上100个集合中各取一个元素组成. ………………3分
的100个元素只能从以上100个集合中各取一个元素组成. ………………3分
∵以上100个集合中,奇数同时出现,且含奇数的集合共50个,
∴集合![]() 的所有元素之和必为偶数. ………………5分
的所有元素之和必为偶数. ………………5分
(2)不妨设![]() 为依次从以上前99个集合中选取的元素,
为依次从以上前99个集合中选取的元素,![]() ,
,
且记各集合的落选元素分别为![]() ,则
,则![]() ,
,![]() ,
,
由于![]() =
=![]()
∴ ![]() +
+![]()
=![]() =
=![]() =2646700,……① ………8分
=2646700,……① ………8分
而![]() +
+![]() =
=![]() ,
,
![]() =10002-100=9902,
=10002-100=9902,
∴ ![]() =19800-9902=9898 ………………10分
=19800-9902=9898 ………………10分
∴ ![]() -
-![]()
=![]() +
+![]() +…+
+…+![]() +
+![]()
=![]() +
+![]() +…+
+…+![]() +
+![]()
=200![]() -
-![]() )+10000
)+10000
=![]() ……② …………………12分
……② …………………12分
由①②得:![]() =1328750 . ………………13分
=1328750 . ………………13分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. 的最小值
的最小值 ;
; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 ,如果
,如果 ,求实数
,求实数 的取值范围.
的取值范围. :函数
:函数 =
=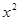 -2
-2 -1在区间(-∞,3]上单调递减;命题
-1在区间(-∞,3]上单调递减;命题 :函数
:函数 的定义域是
的定义域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求
为假命题,求 的取值范围.
的取值范围.
 ,
,
 ,已知
,已知 ,
, ,且△ABC的面积小于
,且△ABC的面积小于 ,求角B的取值范围。
,求角B的取值范围。  .
. 的最小正周期;
的最小正周期;  时,求函数
时,求函数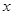 的值.
的值.