题目内容
已知关于 的不等式
的不等式
 .
.
(1)当 时,求此不等式的解集;(2)若此不等式的解集为R,求实数
时,求此不等式的解集;(2)若此不等式的解集为R,求实数 的取值范围.
的取值范围.
(1) (2)
(2)
解析试题分析:(1)理解绝对值的几何意义, 表示的是数轴的上点
表示的是数轴的上点 到原点的距离,由于
到原点的距离,由于 到1、2的距离之和大于2,因此
到1、2的距离之和大于2,因此 不再1和2之间,在1左边和2的右边找.(2)对
不再1和2之间,在1左边和2的右边找.(2)对 分类讨论,分
分类讨论,分 三部分进行讨论;(3)
三部分进行讨论;(3) 的应用.(4)掌握一般不等式的解法:
的应用.(4)掌握一般不等式的解法: ,
, .
.
试题解析:解:(1)当 时,不等式为
时,不等式为 ,
,
由绝对值的几何意义知,不等式的意义可解释为数轴上的点 到1、2的距离之和大于2
到1、2的距离之和大于2
 不等式的解集为
不等式的解集为 .
.
 原不等式解集为R等价于
原不等式解集为R等价于 ,
, 又
又 ,
, .
.
考点:(1)考察绝对值不等式的意义;(2)绝对值不等式的应用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
 的解集为
的解集为 ,则实数
,则实数 的取值范围是____.
的取值范围是____. 的不等式
的不等式 ,其中常数
,其中常数 是实数.
是实数. .
. ,求证:
,求证:
 .
.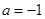 ,
, ,
, 时,求
时,求 的解集;
的解集;  ,且当
,且当 时,
时, 的最小值.
的最小值. +
+ ≥
≥ +
+ .
.