Question

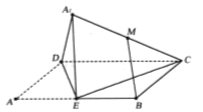
【题目】如图，在三棱锥中，若底面是正三角形，侧棱长，、分别为棱、的中点，并且，则异面直线与所成角为______；三棱锥的外接球的体积为______．

Answer 1

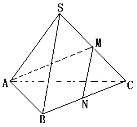
【答案】

【解析】

根据题意得出三棱锥是正三棱锥，易证出平面，再根据，可得，从而得出异面直线与所成角；判断出三棱锥是正方体的一部分，从而得出球的直径，即可得出球的体积.

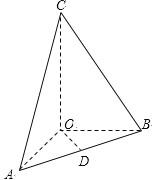
由三棱锥中，若底面是正三角形，侧棱长知，三棱锥是正三棱锥，则点在底面中的投影为底面的中心，为中点如图，

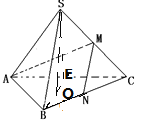
因此,所以平面,平面,

,又、分别为棱、的中点，

则,因此，异面直线与所成角为；

,

平面,又，则平面,又三棱锥是正三棱锥，

因此三棱锥可以看成正方体的一部分且为正方体的四个顶点，故球的直径为，

则球的体积为.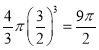

故答案为：；.