题目内容
定义一种运算a⊕b=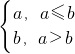 ,令f(x)=(cos2x+sinx)⊕
,令f(x)=(cos2x+sinx)⊕ ,且x∈[0,
,且x∈[0, ],则函数f(x-
],则函数f(x- )的最大值是
)的最大值是
- A.

- B.1
- C.-1
- D.-

A
分析:先比较cos2x+sinx与 的大小,来确定应用哪一段解析式,再研究函数f(x-
的大小,来确定应用哪一段解析式,再研究函数f(x- )的类型选择方法求最大值.
)的类型选择方法求最大值.
解答:由于cos2x+sinx=-sin2x+sinx+1=-(sinx- )2+
)2+ ≤
≤
∴f(x)=(cos2x+sinx)? =cos2x+sinx,
=cos2x+sinx,
f(x- )=cos2(x-
)=cos2(x- )+sin(x-
)+sin(x- )=sin2x-cosx=-(cos2x+cosx+
)=sin2x-cosx=-(cos2x+cosx+ )+1+
)+1+ =-(cosx+
=-(cosx+ )2+
)2+ ≤
≤
故选A
点评:本题是一道定义题,要严格按照定义转化为已有的知识去解决.
分析:先比较cos2x+sinx与
 的大小,来确定应用哪一段解析式,再研究函数f(x-
的大小,来确定应用哪一段解析式,再研究函数f(x- )的类型选择方法求最大值.
)的类型选择方法求最大值.解答:由于cos2x+sinx=-sin2x+sinx+1=-(sinx-
 )2+
)2+ ≤
≤
∴f(x)=(cos2x+sinx)?
 =cos2x+sinx,
=cos2x+sinx,f(x-
 )=cos2(x-
)=cos2(x- )+sin(x-
)+sin(x- )=sin2x-cosx=-(cos2x+cosx+
)=sin2x-cosx=-(cos2x+cosx+ )+1+
)+1+ =-(cosx+
=-(cosx+ )2+
)2+ ≤
≤
故选A
点评:本题是一道定义题,要严格按照定义转化为已有的知识去解决.

练习册系列答案
相关题目
定义一种运算(a*b)=
,则函数f(x)=(2x*2-x)的值域为( )
|
| A、(0,1) |
| B、(0,1] |
| C、[1,+∞) |
| D、(1,+∞) |