题目内容
直线 与圆
与圆 相交的弦长为 。
相交的弦长为 。

解析试题分析:将直线2ρcosθ=1化为普通方程为:2x=1.
∵ρ=2cosθ,∴ρ2=2ρcosθ,化为普通方程为:x2+y2=2x,即(x-1)2+y2=1.结合图形特征知,弦长为2 =
= 。
。
考点:本题主要考查极坐标方程与普通方程的互化,直线与圆的位置关系。
点评:基础题,直线与圆的位置关系问题,往往利用“特征三角形”,研究弦长一半、半径、圆心到直线的距离三者之间的关系。

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
 的圆心到直线
的圆心到直线 的距离是 .
的距离是 . 与直线
与直线 平行,则常数
平行,则常数 的值为_______.
的值为_______. 的圆心的极坐标是
的圆心的极坐标是  ,则
,则 的最大值是 。
的最大值是 。 和
和 的两个圆的圆心距为 ;
的两个圆的圆心距为 ; ,动点
,动点 在直线
在直线 上运动,则线段
上运动,则线段 的最短长度为 .
的最短长度为 .
 极轴为
极轴为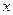 轴正半轴
轴正半轴 的极坐标方程为
的极坐标方程为 ,写出曲线
,写出曲线