题目内容
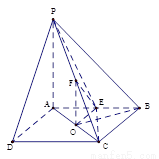
(12分)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
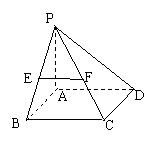 (Ⅰ)证明:EF∥平面PAD;
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求四棱锥E-ABCD的体积V;
(Ⅲ)求二面角E-AD-C的大小.
解:(Ⅰ)∵E,F分别是PB,PC的中点
∴EF∥BC ……………………1分
∵BC∥AD
∴EF∥AD ……………………2分
∵AD![]() 平面PAD,EF
平面PAD,EF![]() 平面PAD
平面PAD
∴EF∥平面PAD ……………………4分
(Ⅱ)(法1)∵AP=AB,BP=2,AP⊥平面ABCD
∴AB=AP=![]() ……………………5分
……………………5分
∵S矩形ABCD=AB·BC=2![]()
∴VP-ABCD=![]() S矩形ABCD·PA=
S矩形ABCD·PA=![]() …………6分
…………6分
∴V=![]() VP-ABCD=
VP-ABCD=![]() ……………………8分
……………………8分
(Ⅱ)(法2)连接EA,EC,ED,过E作EG∥PA交AB于点G
则EG⊥平面ABCD,且EG=![]() PA ………5分
PA ………5分
∵AP=AB,![]() PAB=90°,BP=2
PAB=90°,BP=2
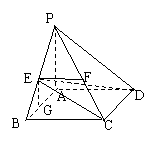 ∴AP=AB=
∴AP=AB=![]() ,EG=
,EG=![]() ………6分
………6分
∵S矩形ABCD=AB·BC
=2![]()
∴V=![]() S矩形ABCD·EG
S矩形ABCD·EG
=![]() ……………………8分
……………………8分
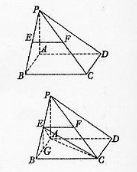 (Ⅲ)∵PA⊥平面ABCD
(Ⅲ)∵PA⊥平面ABCD
∴AD⊥PA
∵ABCD是矩形
∴AD⊥AB
∵AP∩AB=A
∴AD⊥平面ABP
∵AE![]() 平面ABP
平面ABP
∴AD⊥AE
∴∠BAE为所求二面角的平面角……11分
∵△ABP是等腰直角三角形,E是PB中点
∴所求二面角为45° ………………12分

练习册系列答案
相关题目
 中,侧面
中,侧面 是边长 为2的正三角形,且与底面垂直;底面
是边长 为2的正三角形,且与底面垂直;底面 是菱形,
是菱形, ,
, 为
为 的中点.
的中点.
 平面
平面 .
. 中,
中,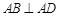 ,
,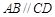 ,
,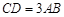 ,平面
,平面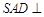 平面
平面 ,
,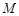 是线段
是线段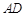 上一点,
上一点,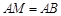 ,
,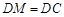 ,
,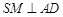 .
.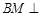 平面
平面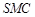 ;
;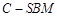 与四棱锥
与四棱锥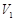 与
与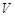 ,求
,求 的值.
的值.
 中,
中, ,
, ,
, ,平面
,平面 平面
平面 ,
, 是线段
是线段 上一点,
上一点, ,
, ,
, .
. 平面
平面 ;
; 与四棱锥
与四棱锥 与
与 ,求
,求 的值.
的值.
