题目内容
(2012•盐城一模)已知整数n≥4,集合M={1,2,3,…,n}的所有3个元素的子集记为A1,A2,…,A
.
(1)当n=5时,求集合A1,A2,…,A
中所有元素之和.
(2)设mi为Ai中的最小元素,设Pn=m1+m2+…+m
,试求Pn.
| C | 3 n |
(1)当n=5时,求集合A1,A2,…,A
| C | 3 5 |
(2)设mi为Ai中的最小元素,设Pn=m1+m2+…+m
| C | 3 n |
分析:(1)由题意可知集合A中的元素,组成集合A的子集的元素,出现的概率相等,求出每个元素出现的次数,即可求出所有元素的和.
(2)若mi为Ai中的最小元素,则应有1≤mi≤n-2,mi∈Z,若1为某个子集的最小元素,则这样的子集个数有
个,若2为某个子集的最小元素,则这个集合中,必不再有1,另外两元素取自剩余的n-2个数字中,有
个,,…,以n-2为最小元素的子集有
个,利用组合数性质
(2)若mi为Ai中的最小元素,则应有1≤mi≤n-2,mi∈Z,若1为某个子集的最小元素,则这样的子集个数有
| C | 2 n-1 |
| C | 2 n-2 |
| C | 2 2 |
解答:解:(1)当n=5时,含元素1的子集中,必有除1以外的两个数字,两个数字的选法有
=6个,所以含有数字1的几何有6个.同理含2,3,4,5的子集也各有6个,
于是所求元素之和为(1+2+3+4+5)×
=6×15=90…(5分)
(2)证明:不难得到1≤mi≤n-2,mi∈Z,并且以1为最小元素的子集有
个,以2为最小元素的子集有
个,以3为最小元素的子集有
,…,以n-2为最小元素的子集有
个,
则Pn=m1+m2+…+m
=1×
+2
+3
+…+(n-2)
…(8分)
=(n-2)
+(n-3)
+(n-4)
+…+
=
+(n-3)(
+
)+(n-4)
+…+
=
+(n-3)(
+
)+(n-4)
+…+
=
+(n-3)
+(n-4)
+…+
=
+
+(n-4)(
+
)+…+
=
+
+(n-4)
+…+
=
+
+
+…+
=
…(10分)
| C | 2 4 |
于是所求元素之和为(1+2+3+4+5)×
| C | 2 4 |
(2)证明:不难得到1≤mi≤n-2,mi∈Z,并且以1为最小元素的子集有
| C | 2 n-1 |
| C | 2 n-2 |
| C | 2 n-3 |
| C | 2 2 |
则Pn=m1+m2+…+m
| C | 3 n |
| C | 2 n-1 |
| C | 2 n-2 |
| C | 2 n-3 |
| C | 2 2 |
=(n-2)
| C | 2 2 |
| C | 2 3 |
| C | 2 n |
| C | 2 n-1 |
| C | 2 2 |
| C | 2 2 |
| C | 2 3 |
| C | 2 4 |
| C | 2 n-1 |
=
| C | 2 2 |
| C | 3 3 |
| C | 2 3 |
| C | 2 4 |
| C | 2 n-1 |
| C | 2 2 |
| C | 3 4 |
| C | 2 4 |
| C | 2 n-1 |
=
| C | 2 2 |
| C | 3 4 |
| C | 3 4 |
| C | 2 4 |
| C | 2 n-1 |
| C | 2 2 |
| C | 3 4 |
| C | 3 5 |
| C | 2 n-1 |
=
| C | 4 4 |
| C | 3 4 |
| C | 3 5 |
| C | 3 n |
| C | 4 n+1 |
点评:本题考查了子集的概念,组合的概念及性质,分类讨论的思想方法,考查推理、计算能力.两题中得出含有相关数字出现的次数是关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
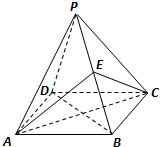 (2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.
(2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.