题目内容
定义:在数列 中,若
中,若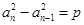 ,(n≥2,n∈N*,p为常数),则称
,(n≥2,n∈N*,p为常数),则称 为“等方差数列”.下列是对“等方差数列”的有关判断:
为“等方差数列”.下列是对“等方差数列”的有关判断:
①若 是“等方差数列”,则数列
是“等方差数列”,则数列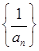 是等差数列;②
是等差数列;②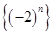 是“等方差数列”;
是“等方差数列”;
③若 是“等方差数列”,则数列
是“等方差数列”,则数列 (k∈N*,k为常数)也是“等方差数列”;
(k∈N*,k为常数)也是“等方差数列”;
④若 既是“等方差数列”,又是等差数列,则该数列是常数数列.
既是“等方差数列”,又是等差数列,则该数列是常数数列.
其中正确的命题为 .(写出所有正确命题的序号)
 中,若
中,若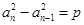 ,(n≥2,n∈N*,p为常数),则称
,(n≥2,n∈N*,p为常数),则称 为“等方差数列”.下列是对“等方差数列”的有关判断:
为“等方差数列”.下列是对“等方差数列”的有关判断:①若
 是“等方差数列”,则数列
是“等方差数列”,则数列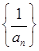 是等差数列;②
是等差数列;②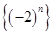 是“等方差数列”;
是“等方差数列”;③若
 是“等方差数列”,则数列
是“等方差数列”,则数列 (k∈N*,k为常数)也是“等方差数列”;
(k∈N*,k为常数)也是“等方差数列”;④若
 既是“等方差数列”,又是等差数列,则该数列是常数数列.
既是“等方差数列”,又是等差数列,则该数列是常数数列.其中正确的命题为 .(写出所有正确命题的序号)
③④
因为①:可以举反例.如an=0时数列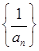 不存在,所以①错误
不存在,所以①错误
②:对数列{(-2)n}有an2-an-12=[(-2)n]2-[(-2)n-1]2=4n-4n-1不是常数,所以②错误
③:对数列{akn}有akn2-ak(n-1)2=(akn2-akn-12)+(akn-12-akn-22)+…+(akn-k+12-akn-k2)=kp,而k,p均为常数,所以数列{akn}也是“等方差数列”,所以③正确
④:设数列{an}首项a1,公差为d则有a2=a1+d,a3=a1+2d,所以有(a1+d)2-a12=p,且(a1+2d)2-(a1+d)2=p,所以得d2+2a1d=p,3d2+2a1d=p,上两式相减得d=0,所以此数列为常数数列,所以④正确.
故答案为:③④
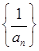 不存在,所以①错误
不存在,所以①错误②:对数列{(-2)n}有an2-an-12=[(-2)n]2-[(-2)n-1]2=4n-4n-1不是常数,所以②错误
③:对数列{akn}有akn2-ak(n-1)2=(akn2-akn-12)+(akn-12-akn-22)+…+(akn-k+12-akn-k2)=kp,而k,p均为常数,所以数列{akn}也是“等方差数列”,所以③正确
④:设数列{an}首项a1,公差为d则有a2=a1+d,a3=a1+2d,所以有(a1+d)2-a12=p,且(a1+2d)2-(a1+d)2=p,所以得d2+2a1d=p,3d2+2a1d=p,上两式相减得d=0,所以此数列为常数数列,所以④正确.
故答案为:③④

练习册系列答案
相关题目
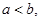 则
则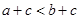 ”. ( 其中
”. ( 其中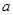 、
、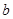 、
、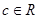 )
) ;命题
;命题 ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。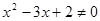 ,则
,则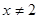 ”的逆否命题为_________
”的逆否命题为_________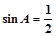 则
则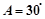
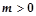 则
则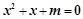 有实根
有实根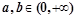 当
当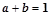 时
时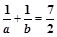
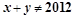 是
是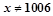 或
或 的充分不必要条件
的充分不必要条件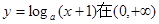 内单调递减;命题Q:曲线
内单调递减;命题Q:曲线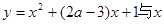 轴交于不同的两点.
轴交于不同的两点. 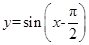 在
在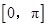 上是减函数;
上是减函数; 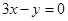 两侧;
两侧; 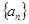 为递减的等差数列,
为递减的等差数列,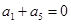 ,设数列
,设数列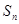 ,则当
,则当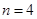 时,
时,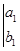
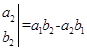 则函数
则函数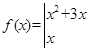
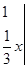 的图象在点
的图象在点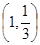 处的切线方程是
处的切线方程是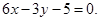 其中正确命题的序号是 (把所有正确命题的序号都写上).
其中正确命题的序号是 (把所有正确命题的序号都写上).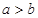 ,则
,则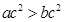 ;(2)直线
;(2)直线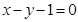 的倾斜角为
的倾斜角为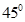 ,纵截
,纵截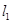 :
: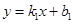 与直线
与直线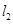 :
: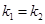 且
且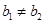 ;
;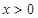 且
且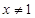 时,
时,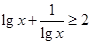 ;(5)到坐标轴距离相等的点的轨迹方程为
;(5)到坐标轴距离相等的点的轨迹方程为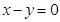 ; 其中真命题的个数是
; 其中真命题的个数是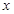 ,使
,使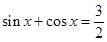 ;②若
;②若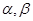 是第一象限角,且
是第一象限角,且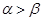 ,则
,则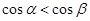 ;
;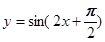 是偶函数; ④函数
是偶函数; ④函数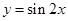 的图象向左平移
的图象向左平移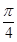 个单位,得到函
个单位,得到函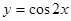 的图象.
的图象.