题目内容
(
(14分)设函数![]() (
(![]() R).
R).
(Ⅰ)当![]() 时,求
时,求![]() 的极值;
的极值;
(Ⅱ)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(Ⅲ)当![]() 时,对于任意正整数n,在区间
时,对于任意正整数n,在区间![]() 上总存在m+4个数
上总存在m+4个数![]()
![]() 使得
使得![]()
![]()
![]() 成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
解析:(Ⅰ)依题意,知![]() 的定义域为
的定义域为![]() .
.
当![]() 时,
时,![]() ,
,![]() .
.
令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
又![]() ,
,
所以![]() 的极小值为
的极小值为![]() ,无极大值 . ………………(3分)
,无极大值 . ………………(3分)
(Ⅱ)![]()
![]() .
.
令![]() ,解得
,解得![]() . ………………(4分)
. ………………(4分)
若![]() ,令
,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
若![]() ,
,
①当![]() 时,
时,![]() ,
,
令![]() ,得
,得![]() 或
或![]() ;
;
令![]() ,得
,得![]() .
.
②当![]() 时,
时,![]() .
.
③当![]() 时,得
时,得![]() ,
,
令![]() ,得
,得![]() 或
或![]() ;
;
令![]() ,得
,得![]() .
.
综上,当![]() 时,
时,![]() 减区间
减区间![]() ,增区间
,增区间![]() .
.
当![]() 时,
时,![]() 减区间为
减区间为![]() ;增区间为
;增区间为![]() .
.
当![]() 时,
时,![]() 减区间为
减区间为![]() .
.
当![]() 时,
时,![]() 减区间为
减区间为![]() ,增区间为
,增区间为![]() . …………………………(9分)
. …………………………(9分)

对所有![]() 满足条件.
满足条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
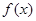 (x∈R)满足
(x∈R)满足 ,
,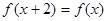 ,则
,则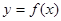 的图象可能是
的图象可能是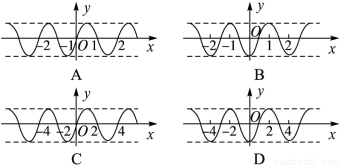
 在R上可导,其导函数为
在R上可导,其导函数为 ,且函数
,且函数 的图象如图所示,则下列结论中一定成立的是 ( )
的图象如图所示,则下列结论中一定成立的是 ( )
 和极小值
和极小值
 和极小值
和极小值 是R上的连续函数,则实数m的值为 ()
是R上的连续函数,则实数m的值为 () ,
, ∈R
∈R 时,
时, 取得极值,求
取得极值,求 内为增函数,求
内为增函数,求