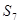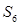题目内容
已知数列 的前n项和
的前n项和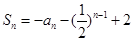 (n为正整数)。
(n为正整数)。
(1)令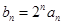 ,求证数列
,求证数列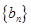 是等差数列,
是等差数列,
(2)求数列 的通项公式;
的通项公式;
(3)令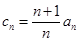 ,
,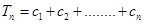 。是否存在最小的正整数
。是否存在最小的正整数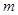 ,使得对于
,使得对于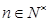 都有
都有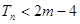 恒成立,若存在,求出
恒成立,若存在,求出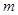 的值。不存在,请说明理由。
的值。不存在,请说明理由。
 的前n项和
的前n项和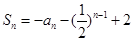 (n为正整数)。
(n为正整数)。(1)令
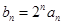 ,求证数列
,求证数列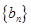 是等差数列,
是等差数列,(2)求数列
 的通项公式;
的通项公式;(3)令
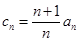 ,
,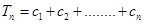 。是否存在最小的正整数
。是否存在最小的正整数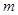 ,使得对于
,使得对于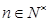 都有
都有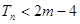 恒成立,若存在,求出
恒成立,若存在,求出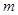 的值。不存在,请说明理由。
的值。不存在,请说明理由。(1)见解析;(2)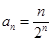 ;(3)4.
;(3)4.
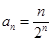 ;(3)4.
;(3)4.(2)中,利用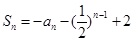 ,对n令值,借助于通项公式与前n项和关系式求解通项公式,令n=1,可得
,对n令值,借助于通项公式与前n项和关系式求解通项公式,令n=1,可得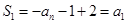 ,即
,即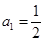 ;当
;当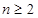 时,
时,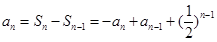 ,得到结论(1)中
,得到结论(1)中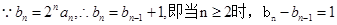
得证数列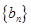 是等差数列,(3)中,
是等差数列,(3)中,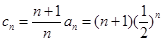 利用错位相减法可得。
利用错位相减法可得。
解:
(1)在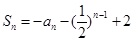 中,令n=1,可得
中,令n=1,可得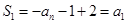 ,即
,即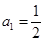
当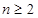 时,
时,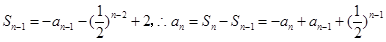 ,
,

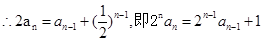 .
.
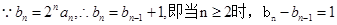 .
.
又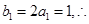 数列
数列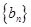 是首项和公差均为1的等差数列. --------5分
是首项和公差均为1的等差数列. --------5分
(2) 于是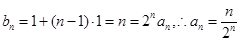 . --------8分
. --------8分
(II)由(I)得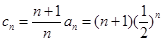 ,所以
,所以
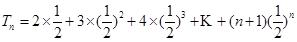
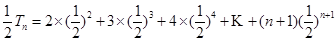
由①-②得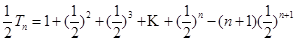
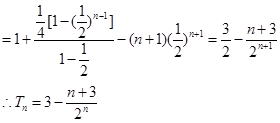 -------12分
-------12分
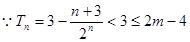
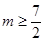
故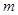 的最小值是4 ------14分
的最小值是4 ------14分
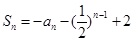 ,对n令值,借助于通项公式与前n项和关系式求解通项公式,令n=1,可得
,对n令值,借助于通项公式与前n项和关系式求解通项公式,令n=1,可得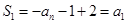 ,即
,即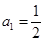 ;当
;当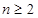 时,
时,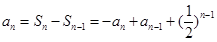 ,得到结论(1)中
,得到结论(1)中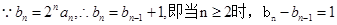
得证数列
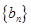 是等差数列,(3)中,
是等差数列,(3)中,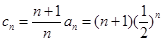 利用错位相减法可得。
利用错位相减法可得。解:
(1)在
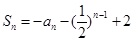 中,令n=1,可得
中,令n=1,可得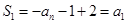 ,即
,即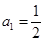
当
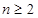 时,
时,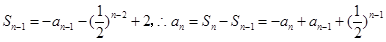 ,
,
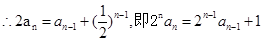 .
.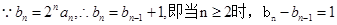 .
. 又
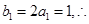 数列
数列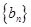 是首项和公差均为1的等差数列. --------5分
是首项和公差均为1的等差数列. --------5分(2) 于是
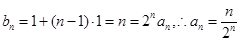 . --------8分
. --------8分(II)由(I)得
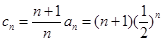 ,所以
,所以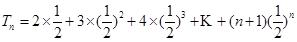
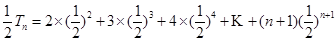
由①-②得
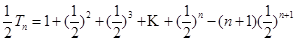
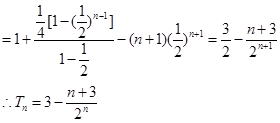 -------12分
-------12分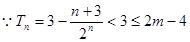
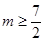
故
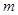 的最小值是4 ------14分
的最小值是4 ------14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
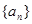 ,满足
,满足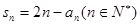
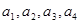 ,并猜想通项公式
,并猜想通项公式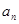 。
。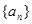 是等差数列,
是等差数列,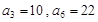 ,数列
,数列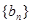 的前n项和是
的前n项和是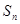 ,且
,且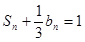 .(1)求数列
.(1)求数列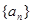 的前
的前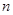 项和
项和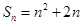 ,设数列
,设数列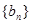 满足
满足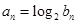 ,
,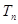 ;
;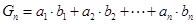 ,求
,求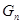 .
.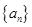 的通项公式
的通项公式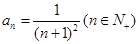 ,
,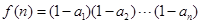 ,试通过计算
,试通过计算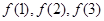 的值,推测出
的值,推测出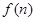 的值。
的值。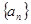 前
前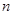 项和为
项和为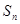 ,且
,且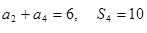
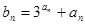 (
(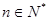 )求数列
)求数列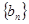 前
前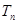
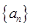 的前n项和
的前n项和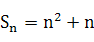 ,在各项为正数的数列
,在各项为正数的数列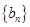 中
中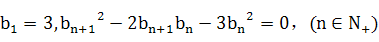
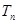
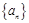 ,其前
,其前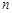 项的和为
项的和为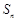 ,且
,且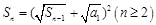 ,若
,若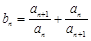 ,且数列
,且数列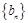 的前
的前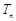 ,则
,则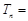 .
.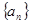 的前
的前 项之和为
项之和为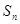 ,已知
,已知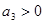 ,
,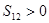 ,
,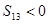 ,则
,则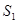 ,
,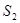 ,
, ,
,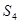 ,…,
,…,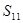 ,
,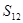 中最大的是 ( )
中最大的是 ( )