题目内容
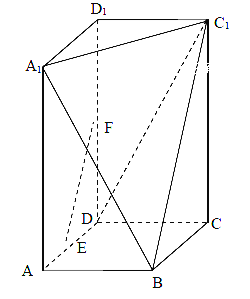
【题目】某中学为了了解全校学生的阅读情况,在全校采用随机抽样的方法抽取了60名学生(其中初中组和高中组各30名)进行问卷调查,并将他们在一个月内去图书馆的次数进行了统计,将每组学生去图书馆的次数分为5组: ![]() ,分别制作了如图所示的频率分布表和频率分布直方图.
,分别制作了如图所示的频率分布表和频率分布直方图.
分组 | 人数 | 频率 |
| 3 | |
| 9 | |
| 9 | |
| 0.2 | |
| 0.1 |
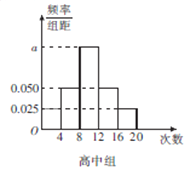
(1)完成频率分布表,并求出频率分布直方图中![]() 的值;
的值;
(2)在抽取的60名学生中,从在一个月内去图书馆的次数不少于16次的学生中随机抽取3人,并用![]() 表示抽得的高中组的人数,求
表示抽得的高中组的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)根据频率分布直方图中矩形和面积为1可求![]() 的值;
的值;
(2)抽得的高中组的人数![]() 服从超几何分布,利用超几何分布的原理列分布列求期望即可.
服从超几何分布,利用超几何分布的原理列分布列求期望即可.
试题解析:
(1)频率分布表如图所示:
分组 | 人数 | 频率 |
| 3 | 0.1 |
| 9 | 0.3 |
| 9 | 0.3 |
| 6 | 0.2 |
| 3 | 0.1 |
由频率分布直方图知![]() ,解得
,解得![]() .
.
(2)由频率分布表知,初中组一个月内去图书馆的次数不少于16次的学生有3人,高中组一个月内去图书馆的次数不少于16次的学生的频率为![]() ,所以,人数为
,所以,人数为![]() 人,
人,
所以![]() 的可能取值为0,1,2,3,
的可能取值为0,1,2,3,
于是![]() ,
,
![]() ,
,
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
使用时间 |
|
|
|
|
|
人数 | 10 | 40 | 25 | 20 | 5 |
(Ⅰ)已知该校大一学生由2400人,求抽取的100名学生中大一学生人数;
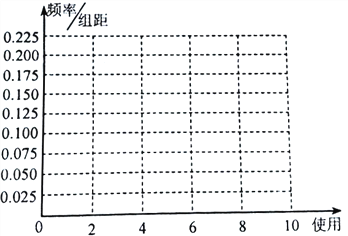
(Ⅱ)作出这些数据的频率分布直方图;
(Ⅲ)估计该校大学生每周使用共享单车的平均时间![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).