题目内容
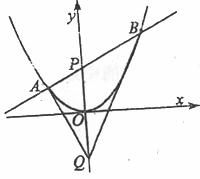
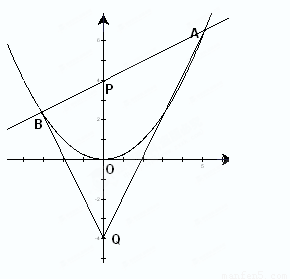
如图,过抛物线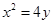 的对称轴上任一点
的对称轴上任一点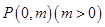 作直线与抛物线交于
作直线与抛物线交于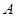 、
、 两点,点Q是点P关于原点的对称点.
两点,点Q是点P关于原点的对称点.
(1)设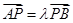 ,证明:
,证明: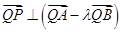 ;
;
(2)设直线AB的方程是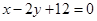 ,过
,过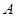 、
、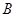 两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
【答案】
(1)详见解析.(2)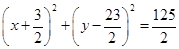 .
.
【解析】
试题分析:(1)将直线与抛物线的方程联立,消去y,得到二次方程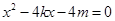 ,应用设而不求,整体代换思想,证明
,应用设而不求,整体代换思想,证明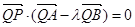 ,进而证明
,进而证明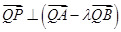 ;(2)将直线与抛物线的方程联立,解出
;(2)将直线与抛物线的方程联立,解出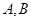 两点的坐标,求出抛物线在点
两点的坐标,求出抛物线在点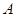 处的切线斜率,则圆心与点
处的切线斜率,则圆心与点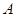 连线的斜率为切线斜率的负倒数,得到方程①,再将
连线的斜率为切线斜率的负倒数,得到方程①,再将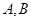 两点的坐标代入到圆的方程中,得到方程②,解方程得到圆心坐标及半径,解出圆的方程.
两点的坐标代入到圆的方程中,得到方程②,解方程得到圆心坐标及半径,解出圆的方程.
试题解析: (1)
由题意,可设直线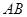 的方程为
的方程为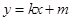 ,代入抛物线方程
,代入抛物线方程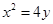 得
得
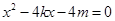 ①
①
设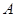 、
、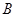 两点的坐标分别是
两点的坐标分别是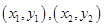 ,则
,则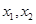 是方程①的两根,所以
是方程①的两根,所以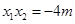
由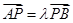 得
得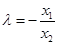 ,又点Q是点P关于原点的对称点,故点Q的坐标为
,又点Q是点P关于原点的对称点,故点Q的坐标为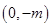 ,从而
,从而
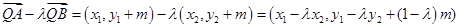
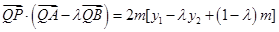
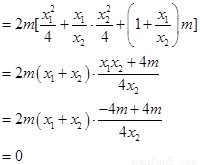
所以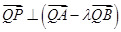
(2) 由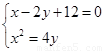 得
得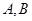 的坐标分别为
的坐标分别为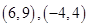
抛物线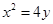 在点A处切线的斜率为3.
在点A处切线的斜率为3.
设圆C的方程是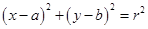 ,则
,则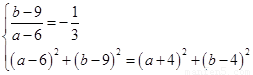
解之得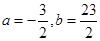
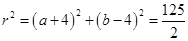
故,圆C的方程是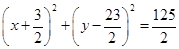
考点:直线与圆锥曲线的位置关系,用数量积表示向量垂直.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.