题目内容
已知函数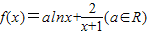 .
.(I)当a=1时,求f(x)在x∈[1,+∞)最小值;
(Ⅱ)若f(x)存在单调递减区间,求a的取值范围;
(Ⅲ)求证:
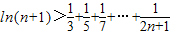 (n∈N*).
(n∈N*).
【答案】分析:(I)可先求f′(x),从而判断f(x)在x∈[1,+∞)上的单调性,利用其单调性求f(x)在x∈[1,+∞)最小值;
(Ⅱ)求h′(x),可得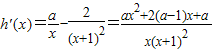 ,若f(x)存在单调递减区间,需h′(x)<0有正数解.从而转化为:ax2+2(a-1)x+a<0有x>0的解.通过对a分
,若f(x)存在单调递减区间,需h′(x)<0有正数解.从而转化为:ax2+2(a-1)x+a<0有x>0的解.通过对a分
a=0,a<0与当a>0三种情况讨论解得a的取值范围;
(Ⅲ)(法一)根据(Ⅰ)的结论,当x>1时,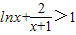 ⇒
⇒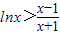 ,再构造函数,令
,再构造函数,令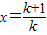 ,有
,有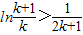 ,从而
,从而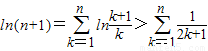 ,问题可解决;
,问题可解决;
(法二)可用数学归纳法予以证明.当n=1时,ln(n+1)=ln2,3ln2=ln8>1⇒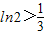 ,成立;设当n=k时,
,成立;设当n=k时,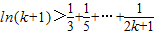 ,再去证明n=k+1时,
,再去证明n=k+1时,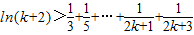 即可(需用好归纳假设).
即可(需用好归纳假设).
解答:解:(I)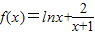 ,定义域为(0,+∞).
,定义域为(0,+∞).
∵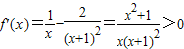 ,
,
∴h(x)在(0,+∞)上是增函数.
当x≥1时,f(x)≥f(1)=1; (3分)
(Ⅱ)∵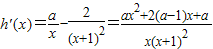 ,
,
∵若f(x)存在单调递减区间,
∴h′(x)<0有正数解.即ax2+2(a-1)x+a<0有x>0的解. (5分)
①当a=0时,明显成立.
②当a<0时,y=ax2+2(a-1)x+a为开口向下的抛物线,ax2+2(a-1)x+a<0总有x>0的解;
③当a>0时,y=ax2+2(a-1)x+a开口向上的抛物线,
即方程ax2+2(a-1)x+a=0有正根.
因为x1x2=1>0,
所以方程ax2+2(a-1)x+a=0有两正根.
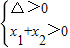 ,解得
,解得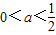 .
.
综合①②③知: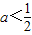 . (9分)
. (9分)
(Ⅲ)
(法一)根据(Ⅰ)的结论,当x>1时,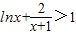 ,即
,即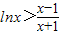 .
.
令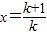 ,则有
,则有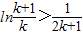 ,
,
∴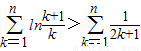 .
.
∵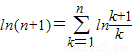 ,
,
∴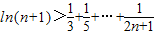 . (12分)
. (12分)
(法二)当n=1时,ln(n+1)=ln2.
∵3ln2=ln8>1,∴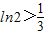 ,即n=1时命题成立.
,即n=1时命题成立.
设当n=k时,命题成立,即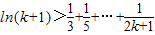 .
.
∴n=k+1时,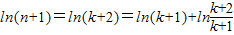
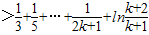 .
.
根据(Ⅰ)的结论,当x>1时,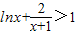 ,即
,即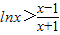 .
.
令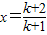 ,则有
,则有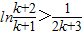 ,
,
则有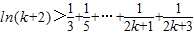 ,即n=k+1时命题也成立.
,即n=k+1时命题也成立.
因此,由数学归纳法可知不等式成立. (12分)
点评:本题考查利用导数研究函数的单调性及数学归纳法,难点之一在于(Ⅱ)中通过求h′(x)后,转化为:ax2+2(a-1)x+a<0有x>0的解的问题,再用分类讨论思想来解决;难点之二在于(Ⅲ)中法一通过构造函数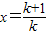 ,用放缩法证得结论,法二通过数学归纳法,其中也有构造函数的思想,属于难题.
,用放缩法证得结论,法二通过数学归纳法,其中也有构造函数的思想,属于难题.
(Ⅱ)求h′(x),可得
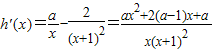 ,若f(x)存在单调递减区间,需h′(x)<0有正数解.从而转化为:ax2+2(a-1)x+a<0有x>0的解.通过对a分
,若f(x)存在单调递减区间,需h′(x)<0有正数解.从而转化为:ax2+2(a-1)x+a<0有x>0的解.通过对a分a=0,a<0与当a>0三种情况讨论解得a的取值范围;
(Ⅲ)(法一)根据(Ⅰ)的结论,当x>1时,
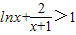 ⇒
⇒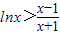 ,再构造函数,令
,再构造函数,令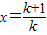 ,有
,有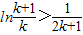 ,从而
,从而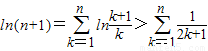 ,问题可解决;
,问题可解决;(法二)可用数学归纳法予以证明.当n=1时,ln(n+1)=ln2,3ln2=ln8>1⇒
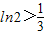 ,成立;设当n=k时,
,成立;设当n=k时,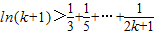 ,再去证明n=k+1时,
,再去证明n=k+1时,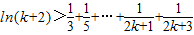 即可(需用好归纳假设).
即可(需用好归纳假设).解答:解:(I)
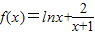 ,定义域为(0,+∞).
,定义域为(0,+∞).∵
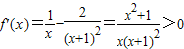 ,
,∴h(x)在(0,+∞)上是增函数.
当x≥1时,f(x)≥f(1)=1; (3分)
(Ⅱ)∵
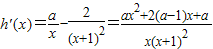 ,
,∵若f(x)存在单调递减区间,
∴h′(x)<0有正数解.即ax2+2(a-1)x+a<0有x>0的解. (5分)
①当a=0时,明显成立.
②当a<0时,y=ax2+2(a-1)x+a为开口向下的抛物线,ax2+2(a-1)x+a<0总有x>0的解;
③当a>0时,y=ax2+2(a-1)x+a开口向上的抛物线,
即方程ax2+2(a-1)x+a=0有正根.
因为x1x2=1>0,
所以方程ax2+2(a-1)x+a=0有两正根.
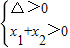 ,解得
,解得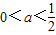 .
.综合①②③知:
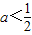 . (9分)
. (9分)(Ⅲ)
(法一)根据(Ⅰ)的结论,当x>1时,
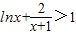 ,即
,即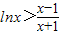 .
.令
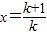 ,则有
,则有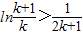 ,
,∴
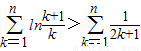 .
.∵
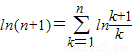 ,
,∴
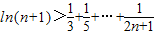 . (12分)
. (12分)(法二)当n=1时,ln(n+1)=ln2.
∵3ln2=ln8>1,∴
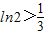 ,即n=1时命题成立.
,即n=1时命题成立.设当n=k时,命题成立,即
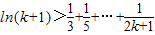 .
.∴n=k+1时,
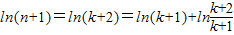
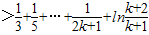 .
.根据(Ⅰ)的结论,当x>1时,
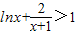 ,即
,即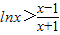 .
.令
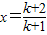 ,则有
,则有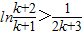 ,
,则有
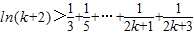 ,即n=k+1时命题也成立.
,即n=k+1时命题也成立.因此,由数学归纳法可知不等式成立. (12分)
点评:本题考查利用导数研究函数的单调性及数学归纳法,难点之一在于(Ⅱ)中通过求h′(x)后,转化为:ax2+2(a-1)x+a<0有x>0的解的问题,再用分类讨论思想来解决;难点之二在于(Ⅲ)中法一通过构造函数
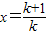 ,用放缩法证得结论,法二通过数学归纳法,其中也有构造函数的思想,属于难题.
,用放缩法证得结论,法二通过数学归纳法,其中也有构造函数的思想,属于难题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. ,
, .
. 。
。 的解集;
的解集;