题目内容
(本小题满分13分)
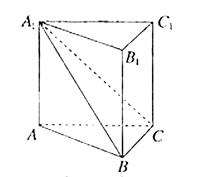
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1.
(Ⅰ)求证:AB⊥BC;
(Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ.判断θ与φ的大小关系,并予以证明.

如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1.
(Ⅰ)求证:AB⊥BC;
(Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ.判断θ与φ的大小关系,并予以证明.
(Ⅰ)证明:如右图,过点A在平面A1ABB1内作
AD⊥A1B于D,则
由平面A1BC⊥侧面A1ABB1,且平面A1BC 侧面A1ABB1=A1B,得
侧面A1ABB1=A1B,得
AD⊥平面A1BC,又BC 平面A1BC,
平面A1BC,
所以AD⊥BC. ……………………………………………………...2分
因为三棱柱ABC—A1B1C1是直三棱柱,
则AA1⊥底面ABC,
所以AA1⊥BC.……………………………………………..……..…3分
又AA1 AD=A,从而BC⊥侧面A1ABB1,
AD=A,从而BC⊥侧面A1ABB1,
又AB 侧面A1ABB1,故AB⊥BC. ………………………..…...4分
侧面A1ABB1,故AB⊥BC. ………………………..…...4分
(Ⅱ)解法1:连接CD,则由(Ⅰ)知 是直线AC与平面A1BC所成的角,……………………………………….………………...6分
是直线AC与平面A1BC所成的角,……………………………………….………………...6分
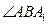 是二面角A1—BC—A的平面角,即
是二面角A1—BC—A的平面角,即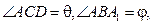
于是在Rt△ADC中, 在Rt△ADB中,
在Rt△ADB中,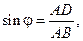 …...8分
…...8分
由AB<AC,得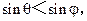 ………………………………….……...11分
………………………………….……...11分
又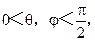 所以
所以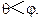 .…………………………………………....13分
.…………………………………………....13分

AD⊥A1B于D,则
由平面A1BC⊥侧面A1ABB1,且平面A1BC
 侧面A1ABB1=A1B,得
侧面A1ABB1=A1B,得AD⊥平面A1BC,又BC
 平面A1BC,
平面A1BC,所以AD⊥BC. ……………………………………………………...2分
因为三棱柱ABC—A1B1C1是直三棱柱,
则AA1⊥底面ABC,
所以AA1⊥BC.……………………………………………..……..…3分
又AA1
 AD=A,从而BC⊥侧面A1ABB1,
AD=A,从而BC⊥侧面A1ABB1,又AB
 侧面A1ABB1,故AB⊥BC. ………………………..…...4分
侧面A1ABB1,故AB⊥BC. ………………………..…...4分(Ⅱ)解法1:连接CD,则由(Ⅰ)知
 是直线AC与平面A1BC所成的角,……………………………………….………………...6分
是直线AC与平面A1BC所成的角,……………………………………….………………...6分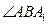 是二面角A1—BC—A的平面角,即
是二面角A1—BC—A的平面角,即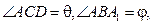
于是在Rt△ADC中,
 在Rt△ADB中,
在Rt△ADB中,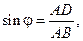 …...8分
…...8分由AB<AC,得
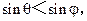 ………………………………….……...11分
………………………………….……...11分又
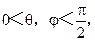 所以
所以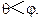 .…………………………………………....13分
.…………………………………………....13分
练习册系列答案
相关题目
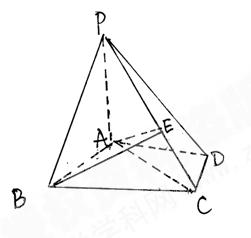
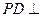 底面ABCD,底面ABCD为正方形,E为PC的中点,点G在BC边上且
底面ABCD,底面ABCD为正方形,E为PC的中点,点G在BC边上且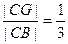 。
。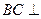 平面PCD;
平面PCD;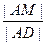 的值。
的值。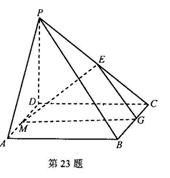

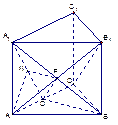
 BD = O,A1C1
BD = O,A1C1 B1D1 = O1,E是O1A的中点.(1) 求二面角O1-BC-D的大小;
B1D1 = O1,E是O1A的中点.(1) 求二面角O1-BC-D的大小;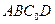 中,
中,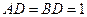 ,
,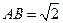 。沿它的对角线
。沿它的对角线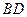 把△
把△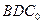 折起,使点
折起,使点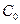 到达平面
到达平面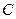 的位置。
的位置。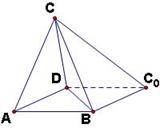
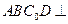 平面
平面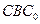 ;
;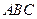 为等腰三角形,求二面角
为等腰三角形,求二面角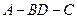 的大小。
的大小。 ,有以下几个判断:
,有以下几个判断: 若
若 ,则
,则 ;
; 若
若 ,则
,则 ;
; 若
若 ,则
,则 若
若






 π
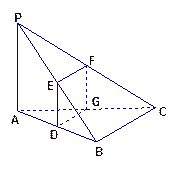
π 平面ABCD、M、N、E分别是AB、PC、CD的中点。
平面ABCD、M、N、E分别是AB、PC、CD的中点。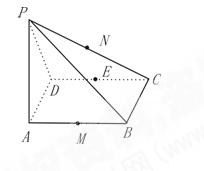
 底面ABCD,AB
底面ABCD,AB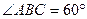 ,PA=AB=BC,E是PC的中点
,PA=AB=BC,E是PC的中点