题目内容
(本小题12分)已知函数f(x)的定义域为(-2,2),f(x)≠0,且对任意实数a, b∈(-2,2)均满足f(a+b)+f(a-b)=2f(a)·f(b)。
(1)求f(0)的值。
(2)判断f(x)的奇偶性并说明理由。
(3)当x∈(-2,0]时,f(x)为增函数,若f(1-m)<f(m)成立,求m的取值范围。
解:(1)由题意知,当a=b=0时,f(0)+f(0)=2f2(0)
而f(0)≠0, ∴f(0)=1
(2)令a=0,b=x∈(-2, 2),则f(x)+f(-x)=2f(0)·f(x)
∴f(-x)=f(x) ∴f(x)为偶函数
(3)函数f(x)在(-2,2)上是偶函数
则由f(1-m)<f(m)得f(|1-m|)<f(|m|)
![]() |1-m|>|m|
|1-m|>|m|
∴ |1-m|<2 即-1<m<![]()
|m|<2

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线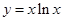
 处的切线方程。
处的切线方程。