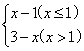题目内容
指出下列函数的不连续点.(1)f(x)=![]() ;
;
(2)f(x)=![]() ;
;
(3)f(x)=![]()
解:(1)由x2-3x+2=0得x=1,x=2.
∴函数的不连续点为x=1和x=2.
(2)当x=kπ(k∈Z)时,tanx=0;当x=kπ+![]() (k∈Z)时,tanx不存在.
(k∈Z)时,tanx不存在.
∴函数f(x)=![]() 的不连续点为x=
的不连续点为x=![]() kπ(k∈Z).
kπ(k∈Z).
(3)f(x)的定义域为(-∞,+∞),
∵![]() f(x)=
f(x)=![]() (x-1)=0,
(x-1)=0,
![]() f(x)=
f(x)=![]() (3-x)=2,
(3-x)=2,
∴![]() f(x)不存在.
f(x)不存在.
∴f(x)在x=1处不连续.
点评:(1)初等函数在其定义域内每一点处都连续.初等函数的无定义点即为函数的不连续点.
(2)分段函数除考虑定义域外,还要考虑在分段点处是否连续.
(3)函数的无定义点,左、右极限不存在或不相等的点,极限值不等于函数值的点都是不连续点.

练习册系列答案
相关题目