题目内容
指出下列函数的不连续点:
(1)f(x)=![]() ;
;
(2)f(x)=![]() ;
;
(3)f(x)=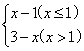
答案:
解析:
提示:
解析:
(1)由x2-3x+2=0,得x=1或x=2,所以函数的不连续点为x=1和x=2. (2)当x=kp(k∈Z)时,tanx=0;当x=kp+ 所以函数f(x)= x=kp和x=kp+ (3)∵ f(x)的定义域为(-∞,+∞) 又 ∴ ∴ f(x)在x=1处不连续 即x=1是此函数的不连续点 |
提示:
由于初等函数在定义域内都连续,所以对初等函数来说,不连续点即是函数无定义的点,而对分段函数(非初等函数)来说,除了无定义的点之外,还要注意分界点. |

练习册系列答案
相关题目


