题目内容
在平面直角坐标系 中,已知
中,已知 分别是椭圆
分别是椭圆 的左、右焦点,椭圆
的左、右焦点,椭圆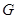 与抛物线
与抛物线 有一个公共的焦点,且过点
有一个公共的焦点,且过点 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆 相交于
相交于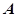 、
、 两点,若
两点,若 (
( 为坐标原点),试判断直线
为坐标原点),试判断直线 与圆
与圆 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
 中,已知
中,已知 分别是椭圆
分别是椭圆 的左、右焦点,椭圆
的左、右焦点,椭圆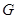 与抛物线
与抛物线 有一个公共的焦点,且过点
有一个公共的焦点,且过点 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设直线
 与椭圆
与椭圆 相交于
相交于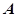 、
、 两点,若
两点,若 (
( 为坐标原点),试判断直线
为坐标原点),试判断直线 与圆
与圆 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.(Ⅰ) (Ⅱ) 直线
(Ⅱ) 直线 与圆
与圆 相切
相切
 (Ⅱ) 直线
(Ⅱ) 直线 与圆
与圆 相切
相切试题分析:(Ⅰ) 由题意得
 ,又
,又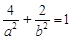 ,结合
,结合 ,可解得
,可解得 的值,从而得椭圆的标准方程.(Ⅱ)设
的值,从而得椭圆的标准方程.(Ⅱ)设 ,则
,则 ,当直线与
,当直线与 轴垂直时,由椭圆的对称性易求
轴垂直时,由椭圆的对称性易求 两点的坐标,并判断直线
两点的坐标,并判断直线 与圆
与圆 是否相切.当直线
是否相切.当直线 的不与
的不与 轴垂直时,可设其方程为
轴垂直时,可设其方程为 ,与椭圆方程联立方程组
,与椭圆方程联立方程组 消法
消法 得:
得: ,
, ,结合
,结合 ,可得
,可得 与
与 的关系,由此可以判断与该直线与圆
的关系,由此可以判断与该直线与圆 的位置关系.
的位置关系.试题解析:解(Ⅰ)由已知得,由题意得
 ,又
,又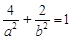 , 2分
, 2分消去
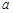 可得,
可得, ,解得
,解得 或
或 (舍去),则
(舍去),则 ,
,所以椭圆
 的方程为
的方程为 . 4分
. 4分(Ⅱ)结论:直线
 与圆
与圆 相切.
相切.证明:由题意可知,直线
 不过坐标原点,设
不过坐标原点,设 的坐标分别为
的坐标分别为
(ⅰ)当直线
 轴时,直线
轴时,直线 的方程为
的方程为 且
且
则
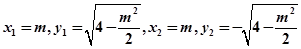


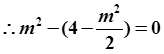
解得
 ,故直线
,故直线 的方程为
的方程为 ,
,因此,点
 到直线
到直线 的距离为
的距离为 ,又圆
,又圆 的圆心为
的圆心为 ,
,半径
 所以直线
所以直线 与圆
与圆 相切 7分
相切 7分(ⅱ)当直线
 不垂直于
不垂直于 轴时,
轴时,设直线
 的方程为
的方程为 ,联立直线和椭圆方程消去
,联立直线和椭圆方程消去 得;
得;得
 ,
,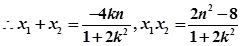



 ,故
,故 ,
,即
 ① 10分
① 10分又圆
 的圆心为
的圆心为 ,半径
,半径 ,
,圆心
 到直线
到直线 的距离为
的距离为 ,
, ② 将①式带入②式得:
② 将①式带入②式得: ,
,所以
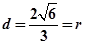 因此,直线
因此,直线 与圆
与圆 相切 13分
相切 13分
练习册系列答案
相关题目
 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,右焦点到直线
,右焦点到直线 =1的距离d=
=1的距离d=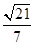 ,O为坐标原点.
,O为坐标原点. (
( >b>0)的离心率e=
>b>0)的离心率e=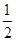 ,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠BDC的值等于 ( )
,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠BDC的值等于 ( ) 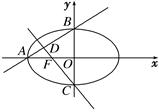
 B.
B. D.
D.
 为椭圆
为椭圆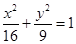 上的一点,
上的一点,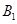 ,
,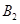 分别为椭圆的上、下顶点,若△
分别为椭圆的上、下顶点,若△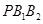 的面积为6,则满足条件的点
的面积为6,则满足条件的点 为焦点在
为焦点在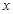 轴上的椭圆,则实数
轴上的椭圆,则实数 ,
, 满足( )
满足( )



 的一条渐近线方程为
的一条渐近线方程为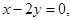 则椭圆
则椭圆 的离心率
的离心率
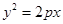 与椭圆
与椭圆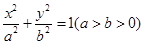 有相同的焦点
有相同的焦点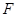 ,
,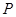 是两曲线的公共点,若
是两曲线的公共点,若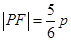 ,则此椭圆的离心率为 .
,则此椭圆的离心率为 .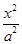 +
+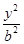 =1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
=1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( ) +
+ =1
=1 +
+ =1
=1 +
+ =1
=1 +
+ =1
=1