题目内容
等差数列{an}的各项均为正数,其前n项和为Sn,满足2S2=a2(a2+1),且a1=1.
(1)求数列{an}的通项公式.
(2)设bn=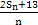 ,求数列{bn}的最小值项.
,求数列{bn}的最小值项.
(1)求数列{an}的通项公式.
(2)设bn=
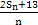 ,求数列{bn}的最小值项.
,求数列{bn}的最小值项.(1) an=n (2) b4=

(1)设数列{an}的公差为d.
由2S2= +a2,
+a2,
可得2(a1+a1+d)=(a1+d)2+(a1+d).
又a1=1,可得d=1(d=-2舍去),∴an=n.
(2)根据(1)得Sn= ,
,
bn=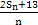 =
= =n+
=n+ +1.
+1.
由于函数f(x)=x+ (x>0)在(0,
(x>0)在(0, ]上单调递减,在[
]上单调递减,在[ ,+∞)上单调递增,
,+∞)上单调递增,
而3< <4,且f(3)=3+
<4,且f(3)=3+ =
= =
= ,
,
f(4)=4+ =
= =
= ,
,
所以当n=4时,bn取得最小值,
且最小值为 +1=
+1= ,
,
即数列{bn}的最小值项是b4= .
.
由2S2=
 +a2,
+a2,可得2(a1+a1+d)=(a1+d)2+(a1+d).
又a1=1,可得d=1(d=-2舍去),∴an=n.
(2)根据(1)得Sn=
 ,
,bn=
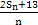 =
= =n+
=n+ +1.
+1.由于函数f(x)=x+
 (x>0)在(0,
(x>0)在(0, ]上单调递减,在[
]上单调递减,在[ ,+∞)上单调递增,
,+∞)上单调递增,而3<
 <4,且f(3)=3+
<4,且f(3)=3+ =
= =
= ,
,f(4)=4+
 =
= =
= ,
,所以当n=4时,bn取得最小值,
且最小值为
 +1=
+1= ,
,即数列{bn}的最小值项是b4=
 .
.
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
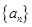 中,已知
中,已知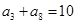 ,则
,则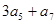 =( )
=( )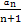 }的前n项和Sn等于 .
}的前n项和Sn等于 . )n,则其前20项和为( )
)n,则其前20项和为( ) (1-
(1- )
) (1-
(1-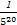 )
) (1-
(1- (1-
(1-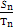 =
=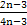 ,则
,则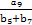 +
+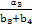 的值为 .
的值为 . =
= +3(n∈N*),则a10=( )
+3(n∈N*),则a10=( )

 和等比数列
和等比数列 满足
满足 则
则 ( )
( )