题目内容
20. 已知正四面体ABCD中,E,F分别是BC,AD的中点,求
已知正四面体ABCD中,E,F分别是BC,AD的中点,求(1)直线EF,AC所成角的大小;
(2)直线AE,CF所成角的大小.
分析 (1)根据正四面体的性质,每条棱都相等,相对的棱互相垂直,可借助中位线,平移直线AC到FG,得到异面直线EF与AC所成的角,
再放入直角三角形EFG中,即可求得.
(2)连接AE,CF,DE,取DE中点M,连接MF,CM,可得出;AE∥FM,直线AE,CF所成角的大小与∠MFC相等,转化为在△FMC中,求解FM=$\frac{\sqrt{3}}{4}$a,CF=$\frac{\sqrt{3}}{2}$a,MC=$\frac{\sqrt{7}}{4}$a,利用余弦定理得出COS∠MFC,即可求解角的大小.
解答 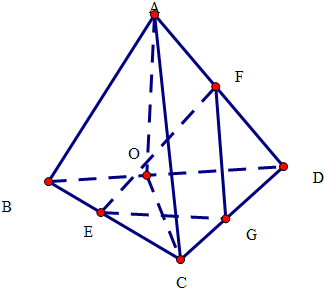 解:(1)取BD中点O,CD中点G,连接AO,CO,EF,EG,FG,
解:(1)取BD中点O,CD中点G,连接AO,CO,EF,EG,FG,
∵正四面体ABCD中,E,F分别是BC,AD的中点,
∴AO⊥DB,CO⊥BD,BD⊥面AOC,
∵AC⊆面AOC,
∴AC⊥DB,
∵E,F,G分别是BC,AD,CD的中点,DB=AC
∴AC∥FG,EG∥BD,$\frac{1}{2}$AC=FG,$\frac{1}{2}BD$=EG
∴FG⊥EG,FG=EG,
∴△EFG为等腰直角三角形,即∠EFG=$\frac{π}{4}$,
直线EF,AC所成角的大小为$\frac{π}{4}$.
(2)连接AE,CF,DE,取DE中点M,连接MF,CM,
∴可得出;AE∥FM,直线AE,CF所成角的大小与∠MFC相等,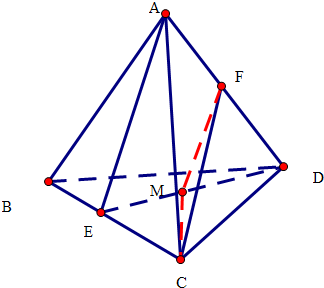 设正四面体ABCD中,棱长为a,则AE=$\frac{\sqrt{3}}{2}$a,FM=$\frac{\sqrt{3}}{4}$a,CF=$\frac{\sqrt{3}}{2}$a,
设正四面体ABCD中,棱长为a,则AE=$\frac{\sqrt{3}}{2}$a,FM=$\frac{\sqrt{3}}{4}$a,CF=$\frac{\sqrt{3}}{2}$a,
∵在Rt△MEC中,EM=$\frac{\sqrt{3}}{4}$a,EC=$\frac{a}{2}$,
∴MC=$\frac{\sqrt{7}}{4}$a,
∵在△FMC中,FM=$\frac{\sqrt{3}}{4}$a,CF=$\frac{\sqrt{3}}{2}$a,MC=$\frac{\sqrt{7}}{4}$a,
∴COS∠MFC=$\frac{M{F}^{2}+F{C}^{2}-M{C}^{2}}{2×MF×FC}$=$\frac{2}{3}$,
∴∠MFC=arccos$\frac{2}{3}$.
故直线AE,CF所成角的大小为arccos$\frac{2}{3}$.
点评 本题主要考查了正四面体中线线位置关系,以及异面直线所成角的求法,综合考查了学生的识图能力,作图能力,以及空间想象力

| 收视情况 | 看直播 | 看转播 | 不看 |
| 人数(单位:人) | 60 | 40 | 20 |
(2)现从(1)所抽取的6人的问卷中每次抽取1份,且不重复抽取,直到确定出所有为看直播的问卷为止,记要抽取的次数为X,求X的分布列及数学期望.
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
 如图,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC的中点,求证:平面EFG∥平面BB1D1D.
如图,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC的中点,求证:平面EFG∥平面BB1D1D.