Question

如图,P为平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点,平面PAD∩平面PBC=m.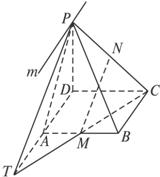

(1)求证:BC∥m;

(2)MN与平面PAD是否平行?试证明你的结论.

Answer 1

剖析:(1)运用线面平行的判定与性质定理;

    (2)在平面PAD上探寻与直线MN平行的直线.

(1)证明:∵BC平面PAD,AD平面PAD,BC∥AD,

    ∴BC∥平面PAD(判定定理).

    而BC平面PBC,平面PBC∩平面PAD=m,

    ∴BC∥m(性质定理).

(2)解:平行.事实上,连结CM并延长,交DA的延长线于T,再连结PT.

    ∵M是平行四边形ABCD的边AB的中点,

    ∴M是TC的中点.

    ∴MN是△TPC的中位线.

    ∴MN∥PT.

    又∵T∈平面PAD,

    ∴PT平面PAD.

    ∴MN∥平面PAD.

讲评:找到平面PAD中的直线PT是解题的关键.实质上这里利用了公理2.