题目内容
已知椭圆的对称轴为坐标轴，离心率
，短轴长为
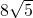，求椭圆的方程．
解：依题意可知2b=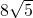，b=
．b2=80
∵
=
∴c=
，a2=b2+c2，所以：a2=144
∴椭圆方程为
或 
故答案为：或 ．
分析：先根据题意求得b，进而根据离心率求得c，a关系，根据a，b和c的关系求得a，即可求出椭圆的方程．
点评：本题主要考查了椭圆的简单性质．在没有注明焦点的位置时，一定要分长轴在x轴和y轴两种情况．
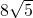，b=．b2=80∵
=∴c=
，a2=b2+c2，所以：a2=144∴椭圆方程为
或 故答案为：
或 ．分析：先根据题意求得b，进而根据离心率求得c，a关系，根据a，b和c的关系求得a，即可求出椭圆的方程．
点评：本题主要考查了椭圆的简单性质．在没有注明焦点的位置时，一定要分长轴在x轴和y轴两种情况．
练习册系列答案
单元期中期末卷系列答案
相关题目
已知椭圆的对称轴为坐标轴，短轴的一个端点和两个焦点的连线构成一个正三角形，且焦点到椭圆上的点的最短距离为
，则椭圆的方程为（ ）
| 3 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
的对称轴为坐标轴,且抛物线
的焦点是椭圆
在椭圆
的方向向量为
、
两点,求
面积的最大值.
，短轴长为4，（1）求椭圆的方程；
两点，求AB的中点坐标及其弦长|AB|。