题目内容
已知球O的半径为2,圆O1是一小圆, ,A、B是圆O1上两点,若∠AO1B=
,A、B是圆O1上两点,若∠AO1B= ,则A,B两点间的球面距离为 ________.
,则A,B两点间的球面距离为 ________.

分析:由题意知应先求出AB的长度,在直角三角形AO1B中由勾股定理可得AB=2由此知三角形AOB是等边三角形,由此可以求出∠AOB的值,进而利用弧长公式求A,B两点间的球面距离.
解答:由题设知
 ,OA=OB=2
,OA=OB=2在圆O1中有
 ,又∠AO1B=
,又∠AO1B=
在直角三角形AO1B中由勾股定理可得AB=2
所以在△AOB中,OA=OB=AB=2,
则△AOB为等边三角形,可得∠AOB=60°
由弧长公式l=rθ(r为半径)得A,B两点间的球面距离lAB=rθ=2×

故答案为

点评:本题的考点是弧长公式,其考查背景是球内一小圆上两点的球面距,对空间想象能力要求较高,此类题是一个基本题型,求解方法固定先求两点间的弦长,再求球心角角,再由弧长公式求弧长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
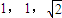 ,若三个小圆所在的平面两两垂直且公共点为P则OP= .
,若三个小圆所在的平面两两垂直且公共点为P则OP= .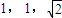 ,若三个小圆所在的平面两两垂直且公共点为P则OP= .
,若三个小圆所在的平面两两垂直且公共点为P则OP= .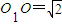 ,A、B是圆O1上两点,若∠AO1B=
,A、B是圆O1上两点,若∠AO1B=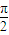 ,则A,B两点间的球面距离为 .
,则A,B两点间的球面距离为 .