题目内容
已知球O的半径为2,圆O1,O2,O3为球O的三个小圆,其半径分别为1,1,
,若三个小圆所在的平面两两垂直且公共点为P则OP=
| 2 |
2
| 2 |
2
.| 2 |
分析:先根据题意求出球心到圆O1,O2,O3的圆心的距离,然后根据三个小圆所在的平面两两垂直且公共点为P,将OP可看成长方体的对角线,最后根据体对角线公式解之即可.
解答:解:根据题意可知球心到圆O1,O2,O3的圆心的距离为
、
、
∵三个小圆所在的平面两两垂直且公共点为P
∴OP可看成长、宽、高分别
、
、
的对角线
∴OP=
=2
故答案为:2
| 3 |
| 3 |
| 2 |
∵三个小圆所在的平面两两垂直且公共点为P
∴OP可看成长、宽、高分别
| 3 |
| 3 |
| 2 |
∴OP=
| 3+3+2 |
| 2 |
故答案为:2
| 2 |
点评:本题主要考查了旋转体的体积,同时考查了空间想象能力和转化能力,属于中档题.

练习册系列答案
相关题目
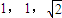 ,若三个小圆所在的平面两两垂直且公共点为P则OP= .
,若三个小圆所在的平面两两垂直且公共点为P则OP= .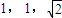 ,若三个小圆所在的平面两两垂直且公共点为P则OP= .
,若三个小圆所在的平面两两垂直且公共点为P则OP= .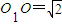 ,A、B是圆O1上两点,若∠AO1B=
,A、B是圆O1上两点,若∠AO1B=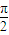 ,则A,B两点间的球面距离为 .
,则A,B两点间的球面距离为 .