题目内容
2.在“中国好声音”的一场海选中,有5位歌手参与评选,有3位导师参与挑选歌手,被导师选中的歌手将归入相应的导师一组,如果一位歌手同时被多位导师选中,则由歌手自己确定归入哪个导师组,如果3位导师都没有选中某位歌手,则该歌手被淘汰,若限定一位导师最多选中3位歌手,那么本场海选结束后,这5位歌手所有可能的结果有210种.分析 根据题意,用排除法分析,首先计算5位歌手被3位导师挑选的全部情况,再计算其中5位歌手被同一个导师挑选与4位歌手被同一个导师挑选的情况数目,由全部情况数目减去5位歌手被同一个导师挑选与4位歌手被同一个导师挑选的情况数目即可得答案.
解答 解:根据题意,5位歌手被3位导师挑选,每个选手都有3种情况,则5位歌手被挑选的情况有3×3×3×3×3=35=243种情况,
而限定一位导师最多选中3位歌手,则需要排除其中5位歌手被同一个导师挑选的情况与4位歌手被同一个导师挑选的情况,
其中5位歌手被同一个导师挑选的情况有3种,
若4位歌手被同一个导师挑选,需要先将5位歌手分成2组,一组4人、一组1人,有C54种分法,
从三位导师中挑选2人,对应这两组,有A32种情况,
则4位歌手被同一个导师挑选的情况有C54×A32=30种,
故若限定一位导师最多选中3位歌手,则一共有243-3-30=210种可能的结果;
故答案为:210.
点评 本题考查计数原理的应用,解题时注意运用排除法分析,可以避免分类讨论,简化计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 一个几何体的三视图如图所示,若该几何体的各顶点都在同一个球面上,则该几何体的侧视图的面积为 ( )
一个几何体的三视图如图所示,若该几何体的各顶点都在同一个球面上,则该几何体的侧视图的面积为 ( )
 一个几何体的三视图如图所示,若该几何体的各顶点都在同一个球面上,则该几何体的侧视图的面积为 ( )
一个几何体的三视图如图所示,若该几何体的各顶点都在同一个球面上,则该几何体的侧视图的面积为 ( )| A. | 4+$\sqrt{2}$ | B. | 4+$\sqrt{3}$ | C. | 3+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
7.已知集合M={1,2},N={x|log2(2x-1)≤2},则M∩N( )
| A. | {1} | B. | {2} | C. | {0,1} | D. | {1,2} |
 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若sin∠ABC=$\frac{2\sqrt{5}}{5}$,PA=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若sin∠ABC=$\frac{2\sqrt{5}}{5}$,PA=10.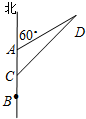 如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.
如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.