题目内容
若a＞1为常数，则关于x的方程
x3-ax2+1=0在区间（0，2）上的实根个数共有（ ）
| 1 |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
分析：由题意a＞1为常数，对方程
x3-ax2+1=0在区间（0，2）进行求导，利用导数判断出函数的大致图象，从而可知它与x轴的交点个数．
| 1 |
| 3 |
解答：解：令f（x）=
x3-ax2+1，
则f′（x）=x2-2ax=x（x-2a），
令f′（x）=0可得，
x=0，或x=2a＞2，
∴f（x）在区间（0，2）上为减函数，
∴f（0）=1＞0，f（2）=
-4a＜0，
∴方程
x3-ax2+1=0在区间（0，2）上的实根个数共有一个，
故选B．
| 1 |
| 3 |
则f′（x）=x2-2ax=x（x-2a），
令f′（x）=0可得，
x=0，或x=2a＞2，
∴f（x）在区间（0，2）上为减函数，
∴f（0）=1＞0，f（2）=
| 11 |
| 3 |
∴方程
| 1 |
| 3 |
故选B．
点评：此题考查根的存在性及个数的判断，解题的关键是利用导数来判断函数在区间（0，2）上的单调性，是一道好题．
练习册系列答案
阅读快车系列答案
相关题目
x3－ax2＋1＝0在区间(0，2)上的实根的个数为________．
在区间（0，2）上的实根个数共有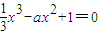
在区间（0，2）上的实根个数共有（ ）