题目内容
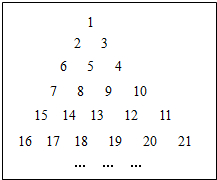 把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,设第n行左侧第一个数为an,如a5=15,则该数列{an}的前n项和Tn(n为偶数)为
把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,设第n行左侧第一个数为an,如a5=15,则该数列{an}的前n项和Tn(n为偶数)为
- A.
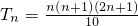
- B.
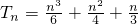
- C.
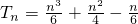
- D.
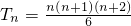
B
分析:方法一:(特值法)根据T2=a1+a2=3,把n=2代入选项,排除C、D,再代入n=4,可判断选项;
方法二:因为当n为奇数时, ,当n为偶数时,an=an-1+1,然后利用分组求和法求出数列{an}的前n项和Tn(n为偶数),可得结论.
,当n为偶数时,an=an-1+1,然后利用分组求和法求出数列{an}的前n项和Tn(n为偶数),可得结论.
解答:方法一:(特值法)因为T2=a1+a2=3,把n=2代入选项,排除C、D,再代入n=4,因为T4=16,B选项满足,故选B.
方法二:因为当n为奇数时, ,当n为偶数时,an=an-1+1,
,当n为偶数时,an=an-1+1,
故n是偶数时,Tn=a1+(a1+1)+a3+(a3+1)+…+an-1+(an-1+1)
=2a1+1+2a3+1+…+2an-1+1
=
=
=(12+1)+(32+3)+…+[(n-1)2+(n-1)]
=[12+32+52+…+(n-1)2]+[1+3+…+(n-1)]
令S=12+22+…+(n-1)2+n2,A=12+32+52+…+(n-1)2,B=22+42+62+…+n2,
A-B=12-22+32-42+52-62+…+(n-1)2-n2=-1-2-3-4-…-(n-1)-n=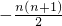 ,
,
又 ,得
,得 =
=
则 Tn=
 =
=
 =
= .
.
故选B.
点评:本题主要考查了数列的求和,以及特殊值法的应用,同时考查了计算能力,属于中档题.
分析:方法一:(特值法)根据T2=a1+a2=3,把n=2代入选项,排除C、D,再代入n=4,可判断选项;
方法二:因为当n为奇数时,
 ,当n为偶数时,an=an-1+1,然后利用分组求和法求出数列{an}的前n项和Tn(n为偶数),可得结论.
,当n为偶数时,an=an-1+1,然后利用分组求和法求出数列{an}的前n项和Tn(n为偶数),可得结论.解答:方法一:(特值法)因为T2=a1+a2=3,把n=2代入选项,排除C、D,再代入n=4,因为T4=16,B选项满足,故选B.
方法二:因为当n为奇数时,
 ,当n为偶数时,an=an-1+1,
,当n为偶数时,an=an-1+1,故n是偶数时,Tn=a1+(a1+1)+a3+(a3+1)+…+an-1+(an-1+1)
=2a1+1+2a3+1+…+2an-1+1
=

=

=(12+1)+(32+3)+…+[(n-1)2+(n-1)]

=[12+32+52+…+(n-1)2]+[1+3+…+(n-1)]

令S=12+22+…+(n-1)2+n2,A=12+32+52+…+(n-1)2,B=22+42+62+…+n2,
A-B=12-22+32-42+52-62+…+(n-1)2-n2=-1-2-3-4-…-(n-1)-n=
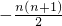 ,
,又
 ,得
,得 =
=
则 Tn=

 =
=
 =
= .
.故选B.
点评:本题主要考查了数列的求和,以及特殊值法的应用,同时考查了计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 (2011•蓝山县模拟)把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,设第n行左侧第一个数为an,如a5=15,则该数列{an}的前n项和Tn(n为偶数)为( )
(2011•蓝山县模拟)把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,设第n行左侧第一个数为an,如a5=15,则该数列{an}的前n项和Tn(n为偶数)为( ) ,如
,如 ,则该数列
,则该数列 的前n项和
的前n项和 (n为偶数)为( )
(n为偶数)为( ) B.
B.
 D.
D.







