题目内容
在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为A(-1,0),B(1,0),平面
内两点G,M同时满足下列条件①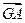 +
+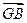 +
+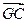 =0;②|
=0;②|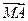 |=|
|=|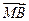 |=|
|=|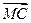 |;③
|;③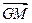 ∥
∥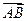 .(Ⅰ)求△ABC的顶点C的轨迹方程;(Ⅱ)是否存在过点P(3,0)的直线l与(Ⅰ)中轨迹交于E、F两点,且OE⊥OF?若存在,求出直线l斜率k的值;若不存在,说明理由.
.(Ⅰ)求△ABC的顶点C的轨迹方程;(Ⅱ)是否存在过点P(3,0)的直线l与(Ⅰ)中轨迹交于E、F两点,且OE⊥OF?若存在,求出直线l斜率k的值;若不存在,说明理由.
内两点G,M同时满足下列条件①
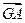 +
+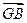 +
+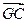 =0;②|
=0;②|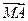 |=|
|=|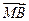 |=|
|=|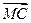 |;③
|;③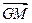 ∥
∥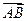 .(Ⅰ)求△ABC的顶点C的轨迹方程;(Ⅱ)是否存在过点P(3,0)的直线l与(Ⅰ)中轨迹交于E、F两点,且OE⊥OF?若存在,求出直线l斜率k的值;若不存在,说明理由.
.(Ⅰ)求△ABC的顶点C的轨迹方程;(Ⅱ)是否存在过点P(3,0)的直线l与(Ⅰ)中轨迹交于E、F两点,且OE⊥OF?若存在,求出直线l斜率k的值;若不存在,说明理由.(Ⅰ) 
 (Ⅱ)
(Ⅱ) 

 (Ⅱ)
(Ⅱ) 
(I)设
 ,
,  点在线段
点在线段 的中垂线上
的中垂线上
由已知 ;又
;又 ∥
∥ ,
, .
.
又 ,
, ,
,
 .
.

 ,
,

 ,
, 顶点
顶点 的轨迹方程为
的轨迹方程为

(II)设直线 方程为:
方程为: ,
, ,
, ,
,
由 消去
消去 得:
得: ①
①
 ,
,  .
.
∵ ∴
∴ 又
又
∴ , 解得:
, 解得:
由方程①知 >
> ,
, ,
,
故符合条件的直线存在,斜率 .
.

 ,
,  点在线段
点在线段 的中垂线上
的中垂线上由已知
 ;又
;又 ∥
∥ ,
, .
.又
 ,
, ,
, .
.
 ,
,
 ,
, 顶点
顶点 的轨迹方程为
的轨迹方程为

(II)设直线
 方程为:
方程为: ,
, ,
, ,
,由
 消去
消去 得:
得: ①
① ,
,  .
.∵
 ∴
∴ 又
又
∴
 , 解得:
, 解得:
由方程①知
 >
> ,
, ,
,故符合条件的直线存在,斜率
 .
.
练习册系列答案
相关题目
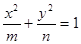 与双曲线
与双曲线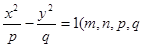 均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则
均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则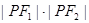 等于 ( )
等于 ( )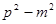
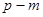
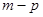
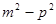
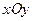 中的抛物线
中的抛物线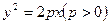 的焦点
的焦点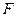 作一条倾斜角为
作一条倾斜角为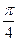 的直线与抛物线相交于A,B两点。
的直线与抛物线相交于A,B两点。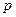 表示A,B之间的距离;
表示A,B之间的距离; 的大小是与
的大小是与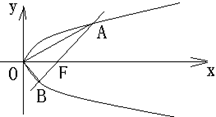
 图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为.
图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为. ,直线
,直线 :
: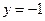 ,
,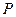 为平面上的动点,过点
为平面上的动点,过点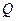 ,且
,且 .
.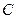 的方程;
的方程;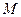 过定点
过定点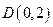 ,圆心
,圆心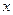 轴交于
轴交于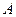 、
、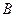 两点,设
两点,设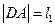 ,
, ,求
,求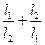 的最大值.
的最大值.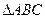 的两个顶点分别
的两个顶点分别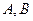 的坐标为
的坐标为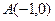 ,
,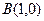 ,平面内两点
,平面内两点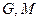 同时满足下列条件:
同时满足下列条件: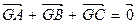 ;②
;②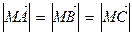 ;③
;③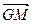 ∥
∥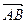
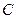 的轨迹方程;
的轨迹方程;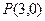 的直线
的直线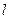 与(1)中轨迹交于
与(1)中轨迹交于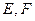 两点,求
两点,求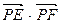 的取值范围
的取值范围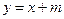 与双曲线
与双曲线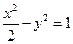 没有公共点,则实数
没有公共点,则实数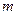 的取值范围是( )
的取值范围是( )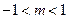
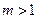 或
或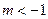
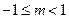
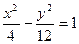 上的动点,F1、F2分别是其左、右焦点,O为坐标原点,则
上的动点,F1、F2分别是其左、右焦点,O为坐标原点,则 的取值范围是 。
的取值范围是 。