题目内容
对实数 和
和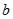 ,定义运算“
,定义运算“ ”:
”: 设函数
设函数 ,
, ,若函数
,若函数 的图像与
的图像与 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数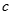 的取值范围是( )
的取值范围是( )
A.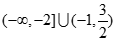 | B. |
C. | D. |
B
解析试题分析:易知 ,在同一坐标内画出f(x)和
,在同一坐标内画出f(x)和 的图像,两个图像交点的个数即为函数
的图像,两个图像交点的个数即为函数 的图像与
的图像与 轴的公共点,由图像知:实数
轴的公共点,由图像知:实数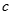 的取值范围是
的取值范围是 。
。
考点:分段函数的图像;二次函数的性质;
点评:函数的零点、对应方程的根、函数图像的交点,三者可以转化。本题就是把“函数 恰与x轴有两个不同的交点”转化为“函数
恰与x轴有两个不同的交点”转化为“函数 和函数
和函数 有两个不同的交点”来做的,体现了转化与化规的数学思想,以及数形结合的数学思想。
有两个不同的交点”来做的,体现了转化与化规的数学思想,以及数形结合的数学思想。

练习册系列答案
相关题目
函数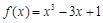 在闭区间 [-3,0] 上的最大值、最小值分别是( )
在闭区间 [-3,0] 上的最大值、最小值分别是( )
| A.1,? 1 | B.1,? 17 | C.3,? 17 | D.9,? 197 |
对任意的 ,则( )
,则( )
A. | B.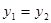 |
C. | D. 的大小不能确定 的大小不能确定 |
定义在R上的偶函数f(x)的一个单调递增区间为(3,5),则y=f(x-1)
| A.图象的对称轴为x=-1,且在(2,4)内递增 |
| B.图象的对称轴为x=-1,且在(2,4)内递减 |
| C.图象的对称轴为x=1,且在(4,6)内递增 |
| D.图象的对称轴为x=1,且在(4,6)内递减 |
已知-2<x<0,则 的最小值为( )
的最小值为( )
| A.2 | B.3 | C. | D.-2 |
函数 ,则f(x)-g(x)是
,则f(x)-g(x)是
| A.奇函数 | B.偶函数 |
| C.既不是奇函数又不是偶函数 | D.既是奇函数又是偶函数 |
已知函数 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
奇函数 在区间
在区间 上是减函数,则
上是减函数,则 在区间
在区间 上是
上是
A.增函数,且最大值为 | B.减函数,且最大值为 |
C.增函数,且最大值为 | D.减函数,且最大值为 |
 ,则函数
,则函数 与
与 的图象是 ( )
的图象是 ( )