题目内容
如果方程
表示双曲线，那么下列椭圆中，与这个双曲线共焦点的是（ ）
A． | B． |
C． | D． |
D
解析试题分析：由方程表示双曲线，可得c=
，判断出A，C不表示椭圆，再求出B，D中的c，即可得出结论．
考点：双曲线与椭圆的标准方程.
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
椭圆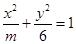
的焦距为2，则m的取值是 （ ）
| A．7 | B．5 | C．5或7 | D．10 |
的焦点相同，且椭圆上任意一点到两焦点的距离之和为
，那么椭圆的离心率等于( )
发出的光线，沿平行于抛物线
的对称轴方向射向此抛物线上的点
，经抛物线反射后，穿过焦点射向抛物线上的点
，再经抛物线反射后射向直线
上的点
，经直线反射后又回到点
，则
等于( )
已知F1、F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|=( )
| A．2 | B．4 | C．6 | D．8 |
设双曲线
-
=1(a>0,b>0)的虚轴长为2,焦距为2
,则双曲线的渐近线方程为( )
A．y=± x | B．y=±2x | C．y=± x | D．y=± x |
已知双曲线
-=1(a>0,b>0)的离心率为,则双曲线的渐近线方程为( )
A．y=± x | B．y=± x |
| C．y=±2x | D．y=±x |
设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
| A．(0,2) | B．[0,2] |
| C．(2,+∞) | D．[2,+∞) |
-y2=1(n>1)的左、右两个焦点为F1,F2,P在双曲线上,且满足|PF1|+|PF2|=2
,则△PF1F2的面积为( )