题目内容
设无穷数列{an}的前n项和为Sn,且 ,p为常数,p<-3.
,p为常数,p<-3.
(1)求证:{an}是等比数列,写出{an}的通项公式;
(2)若数列{an}的公比q=f(p),无穷数列{bn}满足:b1=a1,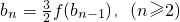 ,求证:
,求证: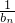 是等差数列,并写出{bn}的通项公式;
是等差数列,并写出{bn}的通项公式;
(3)设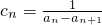 ,在(2)的条件下,有
,在(2)的条件下,有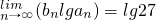 ,求数列{cn}的各项和.
,求数列{cn}的各项和.
解:(1)(3-p)Sn+2pan=3+p,p为常数,且p<-3,n∈N*.
所以(3-p)Sn-1+2pan-1=3+p,(n≥2),两式相减得:(3-p)an+2pan-2pan-1=0 (n≥2)
即:(3+p)an=2pan-1 (n≥2),所以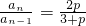 (n≥2)--------------------------2分
(n≥2)--------------------------2分
当n=1时,(3-p)a1+2pa1=3+p,a1=1,故数列{an}是等比数列-----------------------2分
an=( )n-1--------------------------------------------2分
)n-1--------------------------------------------2分
(2)数列{an}的公比q=f(p),q=f(p)= ,b1=a1,bn=
,b1=a1,bn= f(bn-1),(n≥2),
f(bn-1),(n≥2),
所以bn= ?
? =
=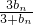 ,所以
,所以 =
= =
= +
+ ,
,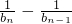 =
= ,b1=a1=1------------------3分
,b1=a1=1------------------3分
数列{ }是等差数列,
}是等差数列, =1+
=1+ (n-1)=
(n-1)= ,所以bn=
,所以bn=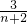 ;----------------2分
;----------------2分
(3)因为an-an+1=( )n-1-(
)n-1-( )n=(
)n=( )n-1[1-
)n-1[1- ]=
]=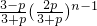
由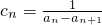 =
=
因为lgan=lg( )n-1=(n-1)lg
)n-1=(n-1)lg ,
,
bnlgan=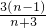 lg
lg
 (bnlgan)=
(bnlgan)= [
[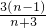 lg
lg ]=3lg
]=3lg
因为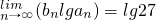 ,所以
,所以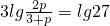 ,p=-9----------------3分
,p=-9----------------3分
所以cn=- (
( )n-1,故{cn}的各项和为S=
)n-1,故{cn}的各项和为S=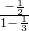 =-
=- .----------------2分.
.----------------2分.
分析:(1)通过 ,通过推出
,通过推出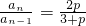 ,即可判断数列是等比数列.
,即可判断数列是等比数列.
(2)利用数列{an}的公比q=f(p),以及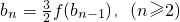 ,求出bn,即可.
,求出bn,即可.
(3)设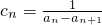 ,在(2)的条件下,推出
,在(2)的条件下,推出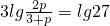 ,求出p,然后求出数列{cn}的各项和.
,求出p,然后求出数列{cn}的各项和.
点评:本题考查数列的判断,数列通项公式的求法,前n项和的求法,数列极限的应用,考查计算能力,转化思想的应用.
所以(3-p)Sn-1+2pan-1=3+p,(n≥2),两式相减得:(3-p)an+2pan-2pan-1=0 (n≥2)
即:(3+p)an=2pan-1 (n≥2),所以
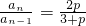 (n≥2)--------------------------2分
(n≥2)--------------------------2分当n=1时,(3-p)a1+2pa1=3+p,a1=1,故数列{an}是等比数列-----------------------2分
an=(
 )n-1--------------------------------------------2分
)n-1--------------------------------------------2分(2)数列{an}的公比q=f(p),q=f(p)=
 ,b1=a1,bn=
,b1=a1,bn= f(bn-1),(n≥2),
f(bn-1),(n≥2),所以bn=
 ?
? =
=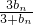 ,所以
,所以 =
= =
= +
+ ,
,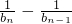 =
= ,b1=a1=1------------------3分
,b1=a1=1------------------3分数列{
 }是等差数列,
}是等差数列, =1+
=1+ (n-1)=
(n-1)= ,所以bn=
,所以bn=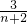 ;----------------2分
;----------------2分(3)因为an-an+1=(
 )n-1-(
)n-1-( )n=(
)n=( )n-1[1-
)n-1[1- ]=
]=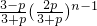
由
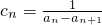 =
=
因为lgan=lg(
 )n-1=(n-1)lg
)n-1=(n-1)lg ,
,bnlgan=
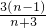 lg
lg
 (bnlgan)=
(bnlgan)= [
[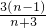 lg
lg ]=3lg
]=3lg
因为
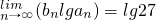 ,所以
,所以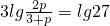 ,p=-9----------------3分
,p=-9----------------3分所以cn=-
 (
( )n-1,故{cn}的各项和为S=
)n-1,故{cn}的各项和为S=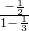 =-
=- .----------------2分.
.----------------2分.分析:(1)通过
 ,通过推出
,通过推出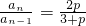 ,即可判断数列是等比数列.
,即可判断数列是等比数列.(2)利用数列{an}的公比q=f(p),以及
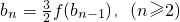 ,求出bn,即可.
,求出bn,即可.(3)设
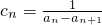 ,在(2)的条件下,推出
,在(2)的条件下,推出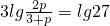 ,求出p,然后求出数列{cn}的各项和.
,求出p,然后求出数列{cn}的各项和.点评:本题考查数列的判断,数列通项公式的求法,前n项和的求法,数列极限的应用,考查计算能力,转化思想的应用.

练习册系列答案
相关题目
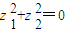 ,则z1=0且z2=0;
,则z1=0且z2=0;