题目内容
在弹性限度内,弹簧所受的压缩力 与缩短的距离
与缩短的距离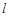 按 胡克定律
按 胡克定律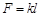 计算.今有一弹簧原长
计算.今有一弹簧原长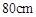 ,每压缩
,每压缩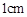 需
需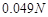 的压缩力,若把这根弹簧从
的压缩力,若把这根弹簧从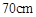 压缩至
压缩至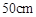 (在弹性限度内),外力克服弹簧的弹力做了( )功(单位:
(在弹性限度内),外力克服弹簧的弹力做了( )功(单位: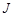 )
)
A.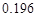 | B. | C.0.686 | D.0.98 |
A
解析试题分析:已知每压缩1cm需0.49N的压缩力,所以由 得
得 ,则把这根弹簧从
,则把这根弹簧从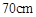 压缩至
压缩至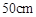 ,外力克服弹簧的弹力做功为
,外力克服弹簧的弹力做功为 ,选A.
,选A.
考点:定积分在物理上的应用

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
对于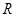 上可导的任意函数
上可导的任意函数 ,若满足
,若满足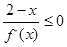 ,则必有( )
,则必有( )
A.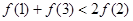 | B.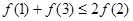 |
C.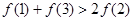 | D.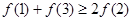 |
函数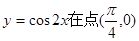 处的切线方程是( )
处的切线方程是( )
A.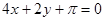 | B.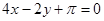 |
C.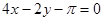 | D.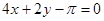 |
函数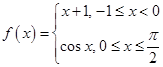 的图象与
的图象与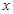 轴所围成的封闭图形的面积为( )
轴所围成的封闭图形的面积为( )
A.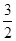 | B.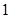 | C. | D. |
若幂函数f(x)的图象过点( ,
,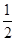 ),则函数g(x)=
),则函数g(x)=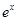 f(x)的单调递减区间为( )
f(x)的单调递减区间为( )
| A.(-∞,0) | B.(-∞,-2) | C.(-2,-1) | D.(-2,0) |
已知函数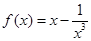 ,则
,则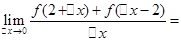 ( )
( )
A.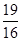 | B.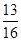 | C.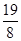 | D.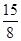 |
已知函数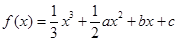 在
在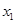 处取得极大值,在
处取得极大值,在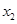 处取得最小值,满足
处取得最小值,满足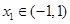 ,
,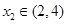 ,则
,则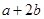 的取值范围是( )
的取值范围是( )
A.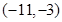 | B.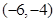 | C.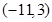 | D. |
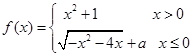 在点(1,2)处的切线与
在点(1,2)处的切线与 的图像有三个公共点,则
的图像有三个公共点,则 的取值范围是( )
的取值范围是( )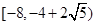

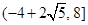
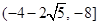

 为
为 的导函数,则
的导函数,则