题目内容
13.已知F1、F2分别是双曲线x2-$\frac{{y}^{2}}{6}$=1的左、右焦点,点P为右支上一点,O为坐标原点,若向量($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)与$\overrightarrow{P{F}_{2}}$的夹角为120°,则点F2到直线PF1的距离为( )| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{21}$ |
分析 以$\overrightarrow{OP}$,$\overrightarrow{O{F}_{2}}$为邻边作平行四边形POF2M,连接OM,则PF1OM是平行四边形,则∠F1PF2=60°,由余弦定理可得|PF2|=4,利用|F2H|=|PF2|sin60°,可得结论.
解答 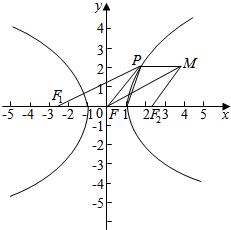 解:以$\overrightarrow{OP}$,$\overrightarrow{O{F}_{2}}$为邻边作平行四边形POF2M,连接OM,则PF1OM是平行四边形,则∠F1PF2=60°,
解:以$\overrightarrow{OP}$,$\overrightarrow{O{F}_{2}}$为邻边作平行四边形POF2M,连接OM,则PF1OM是平行四边形,则∠F1PF2=60°,
F1(-$\sqrt{7}$,0),F2($\sqrt{7}$,0),
设|PF2|=x,则|PF1|=x+2,由余弦定理可得(2$\sqrt{7}$)2=x2+(x+2)2-2x(x+2)×$\frac{1}{2}$,
∴x=4,即|PF2|=4,
∴|F2H|=|PF2|sin60°=2$\sqrt{3}$.
故选:C.
点评 本题考查向量知识的运用,考查余弦定理,考查学生分析解决问题的能力,正确求出|PF2|=4是关键.

练习册系列答案
相关题目
3.已知△ABC的内角∠A、∠B、∠C所对的边分别为a、b、c,且∠A=$\frac{π}{3}$,若a=1,则△ABC的周长l的取值范围是( )
| A. | (1,2) | B. | (1,3] | C. | (2,3] | D. | (1,3) |
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),F1,F2分别是它的左、右焦点,A是它的右顶点,过点F1作一条斜率为k的直线交双曲线于异于顶点的两点M、N,若∠MAN=90°,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
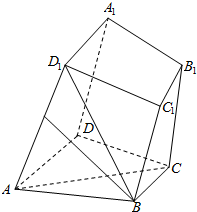 如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1
如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1