题目内容
2.已知函数f(x)=ax-b的反函数为f-1(x),f-1(x)的图象过点(3,2),函数g(x)=log2(3x+b)的图象过点(1,1).(1)求a,b的值;
(2)若f-1(x)≤g(x),求x的取值范围D.
分析 (1)根据互为反函数的图象与性质,列出方程求出a与b的值;
(2)根据f(x)求出f-1(x)的解析式,由f-1(x)≤g(x),列出不等式组,求出解集即可.
解答 解:(1)∵函数f(x)=ax-b的反函数为f-1(x),
且f-1(x)的图象过点(3,2),
∴f(2)=a2-b=3;
又函数g(x)=log2(3x+b)的图象过点(1,1),
∴g(1)=log2(3+b)=1,
即3+b=2,
解得b=-1;
∴a2=3+b=2,
∴a=$\sqrt{2}$或a=-$\sqrt{2}$(舍去),
综上,a=$\sqrt{2}$,b=-1;
(2)∵f(x)=${(\sqrt{2})}^{x}$+1,
∴f-1(x)=${log}_{\sqrt{2}}$(x-1);
又f-1(x)≤g(x),
∴${log}_{\sqrt{2}}$(x-1)≤log2(3x-1),
即${log}_{\sqrt{2}}$(x-1)≤${log}_{\sqrt{2}}$$\sqrt{3x-1}$,
∴$\left\{\begin{array}{l}{x-1>0}\\{3x-1>0}\\{(x-1)≤\sqrt{3x-1}}\end{array}\right.$,
解得1<x≤$\frac{5+\sqrt{17}}{2}$;
∴x的取值范围是(1,$\frac{5+\sqrt{17}}{2}$].
点评 本题考查了不等式的解法与应用问题,也考查了函数的性质与应用问题,考查了转化思想的应用问题,
是基础题目.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
13.已知F1、F2分别是双曲线x2-$\frac{{y}^{2}}{6}$=1的左、右焦点,点P为右支上一点,O为坐标原点,若向量($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)与$\overrightarrow{P{F}_{2}}$的夹角为120°,则点F2到直线PF1的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{21}$ |
17.若函数f(x2+1)的定义域为[-1,1],则f(lgx)的定义域为( )
| A. | [-1,1] | B. | [1,2] | C. | [10,100] | D. | [0,lg2] |
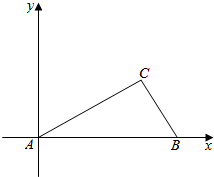 如图,一边在x轴,一个顶点在原点△ABC的所有高都小于1,请问是否存在这样的B、C的位置,使得△ABC的面积大于2015?
如图,一边在x轴,一个顶点在原点△ABC的所有高都小于1,请问是否存在这样的B、C的位置,使得△ABC的面积大于2015?