题目内容
(12分)已知函数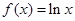 ,
, ,设
,设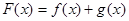 .
.
(1)求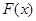 的单调区间;
的单调区间;
(2)若以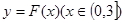 图象上任意一点
图象上任意一点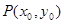 为切点的切线的斜率
为切点的切线的斜率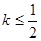
恒成立,求实数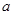 的最小值.
的最小值.
(3)是否存在实数 ,使得函数
,使得函数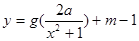 的图象与
的图象与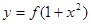 的图
的图
象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
(1) 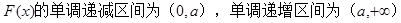
(2)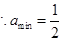 .(3)
.(3)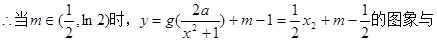
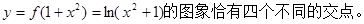
解析试题分析:(1)由题意可知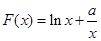 然后直接求导,利用导数大(小)于零求其单调增(减)区间即可.
然后直接求导,利用导数大(小)于零求其单调增(减)区间即可.
(2)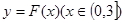 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率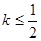
恒成立,其实质是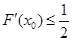 恒成立.即
恒成立.即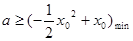
(3)解本小题的关键是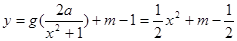 的图象与
的图象与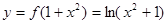 的图象恰有四个不同交点,即
的图象恰有四个不同交点,即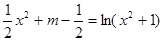 有四个不同的根,
有四个不同的根,
也就是 有四个不同的根,然后再构造函数
有四个不同的根,然后再构造函数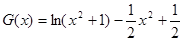
利用导数研究G(x)的单调区间,极值,画出草图,从图像上观察直线y=m在什么范围内有四个不同的交点即可.
(1) 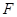
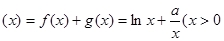
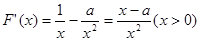
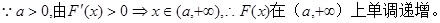
由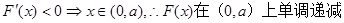 .
.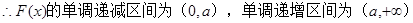
(2)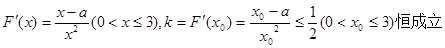
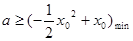 当
当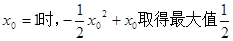
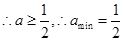 .
.
(3)若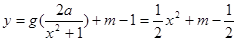 的图象与
的图象与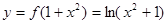 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即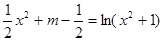 有四个不同的根,亦即
有四个不同的根,亦即 有四个不同的根.
有四个不同的根.
令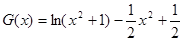 ,
,
则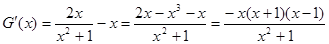 .
.
当 变化时
变化时 的变化情况如下表:
的变化情况如下表: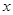
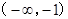
-1 (-1,0) 0 (0,1) 1 (1, 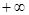 )
)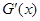
+ 0 - 0 + 0 - 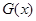
 练习册系列答案
练习册系列答案
单元提优测试卷系列答案
百渡期末综合测试系列答案
聊城中考系列答案
学业测评一卷通小学升学试题汇编系列答案
小学单元综合练习与检测系列答案
实验探究报告练习册系列答案
单元学习体验与评价系列答案
黄冈小状元小学升学考试冲刺复习卷系列答案
毕业总复习冲刺卷系列答案
学习指导系列答案
相关题目
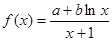 在点
在点 处的切线方程为
处的切线方程为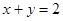 .
. ,
, 的值;
的值; 定义域内的任一个实数
定义域内的任一个实数 ,
,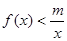 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的最小值为1,且
的最小值为1,且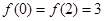 .
.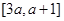 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;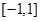 上,
上,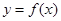 的图象恒在
的图象恒在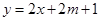 的图象上方,试确定实数
的图象上方,试确定实数 的取值范围.
的取值范围.  =
=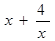
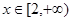 上是增函数;(2)求
上是增函数;(2)求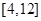 上的值域。
上的值域。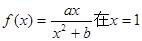 处取得极值2。
处取得极值2。 的解析式;
的解析式;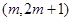 为增函数;
为增函数;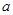 为非负实数,函数
为非负实数,函数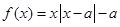 .
.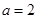 时,求函数的单调区间;
时,求函数的单调区间;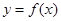 的零点个数.
的零点个数.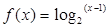 。
。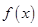 的零点;
的零点;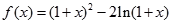 。
。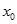 ,使不等式
,使不等式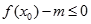 能成立,求实数
能成立,求实数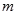 的最小值;
的最小值;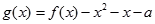 在区间
在区间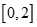 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数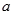 的取值范围。
的取值范围。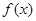 满足以下两个条件:
满足以下两个条件: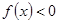 的解集是(-2,0) ②函数
的解集是(-2,0) ②函数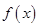 在
在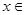
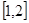 上的最小值是3
上的最小值是3 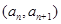
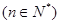 在函数
在函数
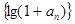 为等比数列
为等比数列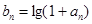 ,是否存在正实数
,是否存在正实数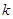 ,使不等式
,使不等式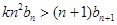 对于一切的
对于一切的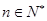 恒成立?若存在,指出
恒成立?若存在,指出