题目内容
已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)探究函数f(x)=ax+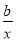 (a、b是正常数)在区间
(a、b是正常数)在区间 和
和 上的单调性(只需写出结论,不要求证明).并利用所得结论,求使方程f(x)-log4m=0有解的m的取值范围.
上的单调性(只需写出结论,不要求证明).并利用所得结论,求使方程f(x)-log4m=0有解的m的取值范围.
(1)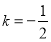 ;
;
(2)函数f(x)=ax+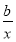 (a、b是正常数)在区间
(a、b是正常数)在区间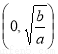 上为减函数,在区间
上为减函数,在区间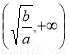 上为增函数;
上为增函数;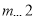 .
.
【解析】
试题分析:(1)由已知函数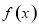 的定义域为
的定义域为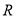 关于原点对称,又是偶函数,则可根据偶函数的定义
关于原点对称,又是偶函数,则可根据偶函数的定义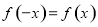 (或者利用特殊值代入计算亦可,如
(或者利用特殊值代入计算亦可,如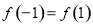 ),得到一个关于
),得到一个关于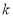 的方程,从而求出
的方程,从而求出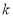 的值;(2)由函数
的值;(2)由函数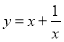 在区间
在区间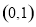 上为减函数,在区间
上为减函数,在区间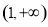 上为增函数,结合是可知函数
上为增函数,结合是可知函数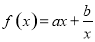 在区间
在区间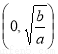 上为单调递减函数,在区间
上为单调递减函数,在区间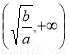 上为单调递增函数.由题意知方程
上为单调递增函数.由题意知方程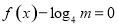 ,即为方程
,即为方程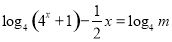 ,若使方程有解,则对数式
,若使方程有解,则对数式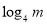 的值要在函数
的值要在函数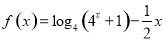 的值域范围内,所以首先要求出函数
的值域范围内,所以首先要求出函数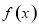 的值域,对函数
的值域,对函数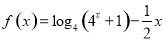 进行化归得
进行化归得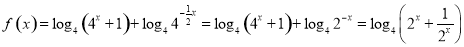 ,故原方程可化为
,故原方程可化为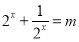 ,令
,令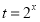 ,
,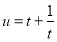 ,则
,则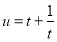 在区间
在区间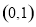 上为减函数,在区间
上为减函数,在区间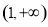 上为增函数,故函数
上为增函数,故函数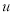 的最小值为
的最小值为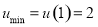 ,即当
,即当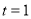 ,
,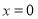 时函数
时函数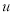 的值,所以函数
的值,所以函数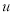 的值域为
的值域为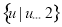 ,从而可求出
,从而可求出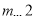 .
.
试题解析:(1)由函数f(x)是偶函数,可知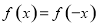 .
.
∴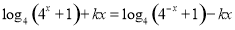 .
.
即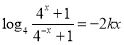 , 2分
, 2分 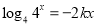 , 4分
, 4分
∴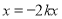 对一切
对一切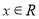 恒成立.∴
恒成立.∴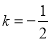 . 5分
. 5分
(注:利用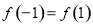 解出
解出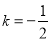 ,亦可得满分)
,亦可得满分)
(2)结论:函数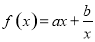 (a、b是正常数)在区间
(a、b是正常数)在区间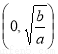 上为减函数,
上为减函数,
在区间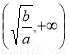 上为增函数. 6分
上为增函数. 6分
由题意知,可先求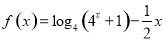 的值域,
的值域,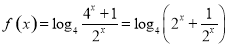 . 8分
. 8分
设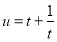 ,又设
,又设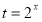 ,则
,则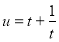 ,由定理,知
,由定理,知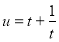 在
在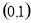 单调递减,在
单调递减,在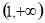 单调递增,所以
单调递增,所以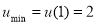 , 11分
, 11分
∵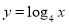 为增函数,由题意,只须
为增函数,由题意,只须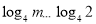 ,即
,即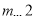
故要使方程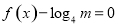 有解,
有解,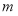 的取值范围为
的取值范围为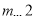 . 13分
. 13分
考点:1.偶函数;2.对数函数;3.函数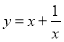 ;4.复合函数值域.
;4.复合函数值域.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目








































