Question

【题目】设，，其中实数

（1）若，求函数的单调区间；

（2）若函数与的图象只有一个公共点，且存在最小值时，记的最小值为，求的值域；

（3）若与均在区间内为增函数，求的取值范围。

Answer 1

【答案】（1）递减区间为；递增区间为（2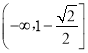）．（3）a≤﹣3或a≥1．

【解析】

（1）由f'（x）＝3x2+2ax﹣a2＝（3x﹣a）（x+a），a＞0，由f′（x）＞0，得x．由此能求出f（x）的单调区间．

（2）g（x）对称轴为，当a＞0时，a且a；当a＜0时，a+2且a+2．由此能求出实数a的取值范围．

（3）由已知条件知x3﹣（a2﹣2）x＝0只有一个实根，得到a的范围，再利用二次函数y＝g（x）有最小值，由此能求出h（a）的值域．

（1）∵f（x）＝x3+ax2﹣a2x+1，

∴f'（x）＝3x2+2ax﹣a2＝（3x﹣a）（x+a），

∵a＞0，∴由f′（x）＞0，得x．

∴f（x）的递减区间为；

递增区间为

（2）由函数y＝f（x），y＝g（x）关于x方程：x3+ax2﹣a2x+1＝ax2﹣2x+1，

即x3﹣（a2﹣2）x＝0只有一个实根，x=0满足题意，

∴x2﹣（a2﹣2）＝0在x时无根，

∴a2﹣2≤0，解得．

二次函数y＝g（x）存在最小值，

∴a＞0，∴

∵g（x）＝ax2﹣2x+1＝a（x）21，

∴，∴h（a）的值域为．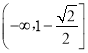

（3）∵g（x）＝ax2﹣2x+1＝a（x）21，

∴对称轴为，

当a＞0时，由（1）知f（x）的递增区间为，

∵g（x）在递增，

依题意，

且（a，a+2）（），∴a且a，解得a≥1．

当a＜0时，f（x）的递增区间为，

g（x）在递增，

依题意且（a，a+2）（﹣∞，），

∴a+2且a+2，解得a≤﹣3．

∴实数a的取值范围为a≤﹣3或a≥1．