题目内容
已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]()
(1)求![]() 的值; (2)求数列
的值; (2)求数列![]() 的通项公式;
的通项公式;
(3)若![]() 的前n项和为
的前n项和为![]() 求满足不等式
求满足不等式![]() 的最小n值.
的最小n值.
解:(1)因为![]() 解得
解得![]()
再分别令n=2,n=3,解得![]()
(2)因为![]() 所以
所以![]() [来源:高&考%资(源#网]两式相减得
[来源:高&考%资(源#网]两式相减得![]()
所以![]()
又因为![]() ,所以
,所以![]() 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列
所以![]() ,所以
,所以![]()
(3)因为![]() ,所以
,所以![]()
所以![]() ①
①
![]() ②
②
①—②得:![]() [来源:Ks5u.com]
[来源:Ks5u.com]
![]()
![]()
所以![]()
若![]() 则
则![]() [来源:高&考%资(源#网KS5U.COM]
[来源:高&考%资(源#网KS5U.COM]
即![]() 所以
所以![]() ,解得
,解得![]() ,
,
所以满足不等式![]() 的最小n值6,
的最小n值6,

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 求使不等式
求使不等式 的前n项和为
的前n项和为 ,
, 且满足
且满足 +n (n>1且n∈
+n (n>1且n∈ )
) ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值  的前n项和为
的前n项和为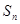 ,且
,且 ,
, ,并猜想
,并猜想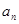 的表达式。
的表达式。