Question

【题目】如图，该几何体由半圆柱体与直三棱柱构成，半圆柱体底面直径，，，D为半圆弧的中点，若异面直线BD和所成角的大小为．

（1）证明：平面；

（2）求该几何体的表面积和体积；

（3）求点D到平面的距离．

Answer 1

【答案】（1）见解析（2）表面积为，体积为，（3）

【解析】

（1）先根据弧中点性质得,再根据直三棱柱性质得,最后根据线面垂直判定定理证结果，

（2）建立空间直角坐标系，根据异面直线BD和所成角利用向量数量积解得棱柱的高，再根据圆柱侧面积、柱体体积公式求几何体的表面积和体积；

（3）利用等体积法求点D到平面的距离．

（1）因为D为半圆弧的中点，所以，

因为直三棱柱,所以平面，

因为平面,所以

因为平面,所以平面；

（2）以A为坐标原点，AC,AB,AA1所在直线为x,y,z轴建立空间直角坐标系，设棱柱的高为则

因为异面直线BD和所成角的大小为，所以

几何体的表面积为

几何体的体积为

（3）因为直三棱柱,所以平面，

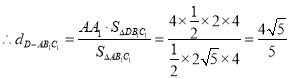
即点D到平面的距离为