Question

如图，已知正三棱柱ABC-A₁B₁C₁的侧棱长和底面边长均为1，M是底面BC边上的中点，N是侧棱CC₁上的点，且CN＝2C₁N.

（Ⅰ）求二面角B₁－AM－N的平面角的余弦值；

（Ⅱ）求点B₁到平面AMN的距离。

Answer 1

解法1：（Ⅰ）因为M是底面BC边上的中点，所以AMBC，又AMCC₁,所以AM面BCC₁B₁，从而AM⊥B₁M, AMNM，所以∠B₁MN为二面角，B₁-AM-N的平面角。又,,

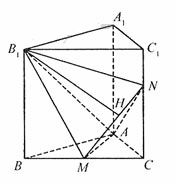            连B₁N，得，

在B₁MN中，由余弦定理得。故所求二面角B₁-AM-N的平面角的余弦值为。

（Ⅱ）过B₁在面BCC₁B₁内作直线B₁H⊥MN，H为垂足。又AM⊥平面BCC₁B₁，所以AMB₁H。于是B₁H平面AMN，故B₁H即为B₁到平面AMN的距离。在R₁△B₁HM中，B₁H＝B₁MsinB₁MH=。故点B₁到平面AMN的距离为1。

解法2：（Ⅰ）建立如图所示的空间直角坐标系，则B₁（0，0，1），M（0，，0）,

C(0,1,0), N (0,1,) , A ()，

所以， 。

因为

所以,同法可得。

故为二面角B₁-AM-N的平面角

∴

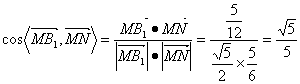
故所求二面角B₁-AM-N的平面角的余弦值为。

（Ⅱ）设为平面AMN的一个法向量，则由得

 

故可取

设与的夹角为，则。

所以B₁到平面AMN的距离为。