题目内容
在平面直角坐标系中,O为坐标原点,点F、T、M、P满足(1)当t变化时,求点P的轨迹C的方程;
(2)若过点F的直线交曲线C于A、B两点,求证:直线TA、TF、TB的斜率依次成等差数列.
(1)解:设点P的坐标为(x,y),
由![]() =
=![]() ,得点M是线段FT的中点,则M(0,
,得点M是线段FT的中点,则M(0,![]() ),
), ![]() =(-x,
=(-x,![]() -y).
-y).
又![]() =
=![]() -
-![]() =(-2,t),
=(-2,t), ![]() =(-1-x,t-y),
=(-1-x,t-y),
由![]() ⊥
⊥![]() ,得2x+t(
,得2x+t(![]() -y)=0. ①
-y)=0. ①
由![]() ∥
∥![]() ,得(-1-x)×0+(t-y)×1=0,∴t=y. ②
,得(-1-x)×0+(t-y)×1=0,∴t=y. ②
由①②消去t,得y2=4x即为所求点P的轨迹C的方程.
(2)证明:设直线TA、TF、TB的斜率依次为k1,k,k2,并记A(x1,y1),B(x2,y2),则k=-![]() .
.
设直线AB的方程为x=my+1,
由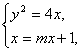 得y2-4my-4=0.
得y2-4my-4=0.
∴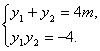
∴y12+y22=(y1+y2)2-2y1y2=16m2+8.
∴k1+k2=![]() +
+![]()
=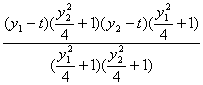 =
=![]()
=-t=2k.
∴k1,k,k2成等差数列.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目