题目内容
已知tanα=
思路分析:因为α+2β=(α+β)+β,也可以把α+2β看成α角和2β角的和.只需先求tan2β即可.
解:∵tanα=![]() ,tanβ=
,tanβ=![]() ,
,
∴tan(α+β)=![]()
=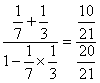 =
=![]() .
.
又∵α,β均为锐角,∴α+β∈(0,π).
而tan(α+β)=![]() >0,∴α+β∈(0,
>0,∴α+β∈(0,![]() ).
).
∴α+2β=(α+β)+β∈(0,π).
∴tan(α+2β)=tan[(α+β)+β]
=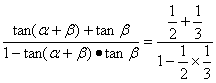 =1.
=1.
∴α+2β=![]() .
.

练习册系列答案
相关题目
题目内容
已知tanα=
思路分析:因为α+2β=(α+β)+β,也可以把α+2β看成α角和2β角的和.只需先求tan2β即可.
解:∵tanα=![]() ,tanβ=
,tanβ=![]() ,
,
∴tan(α+β)=![]()
=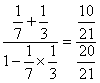 =
=![]() .
.
又∵α,β均为锐角,∴α+β∈(0,π).
而tan(α+β)=![]() >0,∴α+β∈(0,
>0,∴α+β∈(0,![]() ).
).
∴α+2β=(α+β)+β∈(0,π).
∴tan(α+2β)=tan[(α+β)+β]
=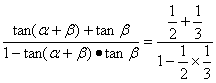 =1.
=1.
∴α+2β=![]() .
.
