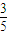题目内容
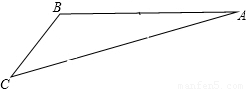
如图,游客从某旅游景区的景点处下山至![]() 处有两种路径. 一种是从沿
处有两种路径. 一种是从沿![]() 直线步行到
直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .
.
现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为50m/min. 在甲出发2min后,乙从
匀速步行,速度为50m/min. 在甲出发2min后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留1min后,再从
处停留1min后,再从![]() 匀速步行到
匀速步行到![]() . 假设缆车匀速直线运动的速度为130m/min,山路
. 假设缆车匀速直线运动的速度为130m/min,山路![]() 长为1260m,经测量,
长为1260m,经测量,![]() ,
,![]() .
.
(1) 求索道![]() 的长;
的长;
(2) 问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3) 为使两位游客在![]() 处相互等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
处相互等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
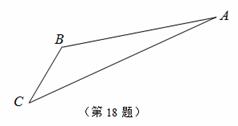
解:(1)

![]()
![]()
![]()
![]()
(2)
![]()
设乙出发![]() 分钟后,甲到了
分钟后,甲到了![]() 处,乙到了E处
处,乙到了E处
则有![]()
![]()
根据余弦定理![]()
即![]()
![]() 当
当![]() 时,
时,![]() 有最小值
有最小值
![]()
(3)设甲所用时间为![]() ,乙所用时间为
,乙所用时间为![]() ,乙步行速度为
,乙步行速度为![]()
由题意![]()
![]()

解不等式得![]()

练习册系列答案
相关题目
 (2013•江苏)如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA=
(2013•江苏)如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA=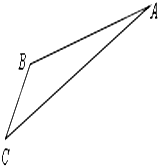 如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为50m/min.乙从A乘缆车到B,在B处停留1min后,再匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA=
如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为50m/min.乙从A乘缆车到B,在B处停留1min后,再匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA=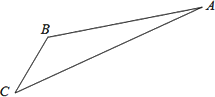
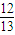 ,cosC=
,cosC=