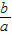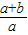Question

设a=log₂6，b=log₄12，c=log₅15，则（　　）

A．c＞b＞a

B．b＞c＞a

C．a＞c＞b

D．a＞b＞c

Answer 1

分析：由对数的单调性可得a＞2＞b＞1，再根据c＞1，利用换底公式可得b＞c，从而得到
a、b、c的大小关系．

解答：解：由于a=log₂6＞log₂4=2；b=log₄12＜log₄16=2，b＞1，∴a＞b．
再根据c=log₅15＞1，c=

lg3+lg5

lg5

=1+

lg3

lg5

；
 b=

lg3+lg4

lg4

=1+

lg3

lg4

，且

lg3

lg5

＜

lg3

lg4

，
可得b＞c．
综上可得，a＞b＞c，
故选 D．

点评：本题主要考查对数值大小的比较，换底公式的应用，属于基础题．