题目内容
设 的最小值是________.
的最小值是________.
2
分析:因为a+b=2,则 =
= (
( )(a+b)=1+
)(a+b)=1+ (
(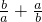 ),利用均值不等式求解.
),利用均值不等式求解.
解答:∵a>0,b>0,a+b=2
∴ =
= (
( )(a+b)=1+
)(a+b)=1+ (
(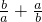 )≥2
)≥2
当且仅当 即a=b=1时取等号
即a=b=1时取等号
∴ 的最小值为2
的最小值为2
故答案为:2
点评:本题考查了利用均值不等式求最值,灵活运用了“1”的代换,是高考考查的重点内容.
分析:因为a+b=2,则
 =
= (
( )(a+b)=1+
)(a+b)=1+ (
(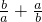 ),利用均值不等式求解.
),利用均值不等式求解.解答:∵a>0,b>0,a+b=2
∴
 =
= (
( )(a+b)=1+
)(a+b)=1+ (
(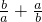 )≥2
)≥2当且仅当
 即a=b=1时取等号
即a=b=1时取等号∴
 的最小值为2
的最小值为2故答案为:2
点评:本题考查了利用均值不等式求最值,灵活运用了“1”的代换,是高考考查的重点内容.

练习册系列答案
相关题目
 的最小值是( )
的最小值是( ) B.
B.  C.
C.  D.
D. 
 的最小值是
的最小值是  的最小值是
的最小值是 B.
B. C.
C. D. 10
D. 10 的最小值是
。
的最小值是
。