题目内容
已知函数 .
.
(1)求函数f(x)的最大值与最小正周期;
(2)求f(x)的单调递增区间.
解:(1)因为函数 ,当
,当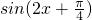 =1时,
=1时,
函数f(x)取到最大值: ,最小正周期T=
,最小正周期T=
(2)函数 的递增区间即是
的递增区间即是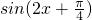 的递增区间.
的递增区间.
由2kπ- ≤2x
≤2x ≤2k
≤2k ,k∈Z 解得kπ
,k∈Z 解得kπ
 ,
,
故f(x)的单调递增区间为[kπ ,k
,k ],k∈Z
],k∈Z
分析:(1)由周期公式和振幅的意义可求周期和最大值;
(2)由符合函数的单调区间把2x+ 当整体来看放在正弦函数的单调递增区间内解不等式可求结果.
当整体来看放在正弦函数的单调递增区间内解不等式可求结果.
点评:本题为三角函数的图象与性质的应用,注意k∈Z容易漏掉,属中档题.
 ,当
,当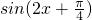 =1时,
=1时,函数f(x)取到最大值:
 ,最小正周期T=
,最小正周期T=
(2)函数
 的递增区间即是
的递增区间即是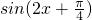 的递增区间.
的递增区间.由2kπ-
 ≤2x
≤2x ≤2k
≤2k ,k∈Z 解得kπ
,k∈Z 解得kπ
 ,
,故f(x)的单调递增区间为[kπ
 ,k
,k ],k∈Z
],k∈Z分析:(1)由周期公式和振幅的意义可求周期和最大值;
(2)由符合函数的单调区间把2x+
 当整体来看放在正弦函数的单调递增区间内解不等式可求结果.
当整体来看放在正弦函数的单调递增区间内解不等式可求结果.点评:本题为三角函数的图象与性质的应用,注意k∈Z容易漏掉,属中档题.

练习册系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.